SOLUTION: Please help me solve this: {{{(12x^2)/(3x^2+12x)}}} divided by {{{(4x^3-36x)/(x^2+x-12)}}}

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Please help me solve this: {{{(12x^2)/(3x^2+12x)}}} divided by {{{(4x^3-36x)/(x^2+x-12)}}}      Log On


   

Question 78331: Please help me solve this:
%2812x%5E2%29%2F%283x%5E2%2B12x%29 divided by %284x%5E3-36x%29%2F%28x%5E2%2Bx-12%29
Found 2 solutions by jim_thompson5910, stanbon:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
%28%2812x%5E2%29%2F%283x%5E2%2B12x%29%29%2F%28%284x%5E3-36x%29%2F%28x%5E2%2Bx-12%29%29 Start with the given expression

%28%2812x%5E2%29%2F%283x%5E2%2B12x%29%29%2A%28%28x%5E2%2Bx-12%29%2F%284x%5E3-36x%29%29 Multiply the 1st fraction by the reciprocal of the 2nd


%28%2812x%5E2%29%2F%283x%5E2%2B12x%29%29%2A%28%28x%5E2%2Bx-12%29%2F%28x%284x%5E2-36%29%29%29 Factor out an x from the denominator of the right term

Factor out an x from the denominator of the left term

Factor the numerator of the 1st term x%5E2%2Bx-12

Solved by pluggable solver: Factoring Quadratics with a leading coefficient of 1 (a=1)
In order to factor 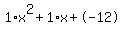1%2Ax%5E2%2B1%2Ax%2B-12, first we need to ask ourselves: What two numbers multiply to -12 and add to 1? Lets find out by listing all of the possible factors of -12


Factors:

1,2,3,4,6,12,

-1,-2,-3,-4,-6,-12,List the negative factors as well. This will allow us to find all possible combinations

These factors pair up to multiply to -12.

(-1)*(12)=-12

(-2)*(6)=-12

(-3)*(4)=-12

Now which of these pairs add to 1? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 1

||||||
First Number|Second Number|Sum
1|-12|1+(-12)=-11
2|-6|2+(-6)=-4
3|-4|3+(-4)=-1
-1|12|(-1)+12=11
-2|6|(-2)+6=4
-3|4|(-3)+4=1
We can see from the table that -3 and 4 add to 1.So the two numbers that multiply to -12 and add to 1 are: -3 and 4 Now we substitute these numbers into a and b of the general equation of a product of linear factors which is: %28x%2Ba%29%28x%2Bb%29substitute a=-3 and b=4 So the equation becomes: (x-3)(x+4) Notice that if we foil (x-3)(x+4) we get the quadratic 1%2Ax%5E2%2B1%2Ax%2B-12 again



Now factor the denominator of the 2nd term 4x%5E2-36

ERROR Algebra::Solver::Engine::invoke_solver_noengine: solver not defined for name 'quadratic_factoring'.
Error occurred executing solver 'quadratic_factoring' .




Basically factors to:




Factor out a 2 out of 2x-6

Notice these terms cancel

Factor a 3 out of 3x%2B12

Notice these terms cancel

So we get after reducing:

%28%2812x%5E2%29%2F%283x%29%29%2A%281%2F%282x%282x%2B6%29%29%29

%28%2812x%5E2%29%2F%286x%5E2%29%282x%2B6%29%29 Now multiply

2%2F%282x%2B6%29 Divide and simplify

2%2F%282%28x%2B3%29%29 Factor out a 2

1%2F%28x%2B3%29 Divide and simplify again. This is your simplified answer.
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
(12x^2)/(3x^2+12x) divided by (4x^3-36x)/(x^2+x-12)
Factor where you can:
(12x^2)/(3x(x+4) / 4x(x+3)(x-3) / (x+4)(x-3)
Cancel where you can to get: invert the denominator and multiply
(4x)/(x+4) * (x+4)/4x(x+3)
Cancel where you can to get:
= 1/(x+3)
===========
Cheers,
Stan H.