Question 781935: An airplane travels 1620 kilometers in the same time a train travels 180 kilometers. If the airplane goes 480 kilometers per hour faster than the train, find the speed of each.
I tried: d=r.t 1620t=180 (t-480)
Please help!
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An airplane travels 1620 kilometers in the same time a train travels 180 kilometers. If the airplane goes 480 kilometers per hour faster than the train, find the speed of each.
I tried: d=r.t 1620t=180 (t-480)
Please help!
Your equation is wrong. It appears as though you wanted to set up a SPEED equation. That would be:  , since the airplane's speed exceeds the train's speed by 480 km/h. This would give you t, or their time, though. You'd then have to calculate the speed after. It's simpler to do the following, naming the variable that's required. That way, you determine the speed of one, from which you'd be able to determine the speed of the other. , since the airplane's speed exceeds the train's speed by 480 km/h. This would give you t, or their time, though. You'd then have to calculate the speed after. It's simpler to do the following, naming the variable that's required. That way, you determine the speed of one, from which you'd be able to determine the speed of the other.
Let speed of plane be S
Then speed of train = S 480
A time equation is thus created, as the time the airplane takes to go 1,620 km is the same time it takes the train to go 180 km. That equation is:

1,620(S 480) = 180S ------ Cross-multiplying
1,620S 777,600 = 180S
1,620S 180S = 777,600
1,440S = 777,600
S, or speed of airplane = 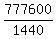 , or , or  km/h km/h
Speed of train = 540 480, or  km/h km/h
You can do the check!!
Further help is available, online or in-person, for a fee, obviously. Send comments, thank-yous, and inquiries to D at MathMadEzy@aol.com
|
|
|