Question 780900: The midpoints of the sides of a triangle are at (0,-3), (-1/2,7/2) and (-7/2,1/2). Find the coordinates of the vertices
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In a message dated 9/5/2013 9:00:27 A.M. Eastern Daylight Time, AnlytcPhil@aol.com writes:
(0,-3), (-1/2,7/2) and (-7/2,1/2)
Plot the points, and connect them:
 These green lines are the mid-segments of the triangle we are trying
to determine the coordinates of.
We remember that a mid-segment of a triangle (which joins the
midpoints of two sides of a triangle) is parallel to the third
side of the triangle. The mid-segment is also 1/2 of the third
side , but we do not need that fact.
Through each of those points we will find the equation of the line
paralell to the mid-segment joining the other two points:
We find the slope of the mid-segment joining
(0,-3) and (
These green lines are the mid-segments of the triangle we are trying
to determine the coordinates of.
We remember that a mid-segment of a triangle (which joins the
midpoints of two sides of a triangle) is parallel to the third
side of the triangle. The mid-segment is also 1/2 of the third
side , but we do not need that fact.
Through each of those points we will find the equation of the line
paralell to the mid-segment joining the other two points:
We find the slope of the mid-segment joining
(0,-3) and ( , , )
m = )
m =  where (x1,y1) = (0,-3)
and where (x2,y2) = (
where (x1,y1) = (0,-3)
and where (x2,y2) = (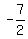 , , )
m = )
m =  = = 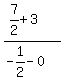 = = 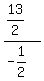 = = 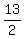 ÷ ÷ = = 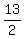 × ×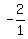 = = 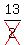 × ×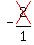 = -13
Now we find the equation of the line through the third point ( = -13
Now we find the equation of the line through the third point (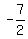 , , ):
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point ( ):
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point (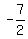 , , )
y - )
y -  = -13(x - ( = -13(x - (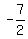 ))
y - ))
y -  = -13(x + = -13(x +  )
y - )
y -  = -13x - = -13x - 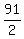 )
y = -13x - )
y = -13x - 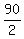 y = -13x - 45
That line is the red one below:
y = -13x - 45
That line is the red one below:
 -------------------
We find the slope of the mid-segment joining
(0,-3) and (
-------------------
We find the slope of the mid-segment joining
(0,-3) and (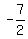 , , )
m = )
m =  where (x1,y1) = (0,-3)
and where (x2,y2) = (
where (x1,y1) = (0,-3)
and where (x2,y2) = (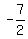 , , )
m = )
m = 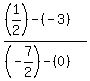 = = 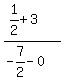 = = 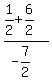 = = 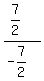 = =  ÷ ÷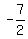 = -1
Now we find the equation of the line through the third point ( = -1
Now we find the equation of the line through the third point ( , , ):
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point ( ):
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point ( , , )
y - )
y -  = -1(x - ( = -1(x - ( ))
y - ))
y -  = -1(x + = -1(x +  )
y - )
y -  = -x - = -x -  )
y = -x + )
y = -x + 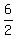 y = -x + 3
That line is the second red one below:
y = -x + 3
That line is the second red one below:
 -------------------
We find the slope of the mid-segment joining
(
-------------------
We find the slope of the mid-segment joining
( , , ) and ( ) and (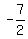 , , )
m = )
m =  where (x1,y1) = (0,-3)
and where (x2,y2) = (
where (x1,y1) = (0,-3)
and where (x2,y2) = (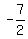 , , )
m = )
m = 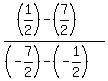 = = 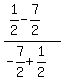 = = 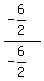 = =  = 1
Now we find the equation of the line through the third point (0,-3), :
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point ( = 1
Now we find the equation of the line through the third point (0,-3), :
Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = the third point ( , , )
y - (-3)} = 1(x - 0)
y + 3 = x
y = x - 3
That line is the second red one below: )
y - (-3)} = 1(x - 0)
y + 3 = x
y = x - 3
That line is the second red one below:
 Now we find the three points of intersection of the three pairs of
the lines
y = -13x - 45, y = -x + 3, y = x - 3
Solve these three systems:
y = -13x - 45 y = -13x - 45 y = -x + 3
y = -x + 3 y = x - 3 y = x - 3
You can do that. They are
(-4,7), (-3,-6), and (3,0)
Edwin
Now we find the three points of intersection of the three pairs of
the lines
y = -13x - 45, y = -x + 3, y = x - 3
Solve these three systems:
y = -13x - 45 y = -13x - 45 y = -x + 3
y = -x + 3 y = x - 3 y = x - 3
You can do that. They are
(-4,7), (-3,-6), and (3,0)
Edwin
|
|
|