remember that a*log(b) = 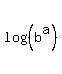
log(x)
log(x) = 2/3 * log(y) = log(y^(2/3)).
Remember if log(a) = log(b) then a=b
x = y^(2/3)
Similarly x = z^(2/5)
y^(2/3) * y^(1/3) = y. y^(1/3) = sqrt(x) so y = x*sqrt(x)
z^(2/5) * z^(2/5) * z^(1/5) = z. z^(2/5) = x, so that's x*x*sqrt(x) = x^2 * sqrt(x).
yz = 