Question 780360: Suppose two trains leave the station at the same time, traveling in opposite directions. One train travels 10 mph faster than the other. In 3.5 hours, the trains are 322 miles apart. Find the speed of each train. Help! Not sure when to use the d=r*t formula or the t=d/r = aaarrrgghhh!!!!!
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Suppose two trains leave the station at the same time, traveling in opposite directions. One train travels 10 mph faster than the other. In 3.5 hours, the trains are 322 miles apart. Find the speed of each train. Help! Not sure when to use the d=r*t formula or the t=d/r = aaarrrgghhh!!!!!
Let slower train's speed be S
Then faster train's speed = S + 10
Create a DISTANCE EQUATION that equates to:
Distance traveled by slower train, in 3.5 hours, plus distance traveled by faster train, in 3.5 hours, equals total distance between them. In algebraic terms, this is translated as:
3.5S + 3.5(S + 10) = 322
3.5S + 3.5S + 35 = 322
7S = 322 - 35
7S = 287
S, or speed of slower train = 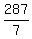 , or , or  mph mph
Speed of faster train = 41 + 10, or  mph mph
You can do the check!!
Further help is available, online or in-person, for a fee, obviously. Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com
|
|
|