f(x) = 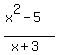 The vertical asymptote is found by setting the denominator = 0
x+3 = 0
x = -3
That is the equation of a vertical line through -3 on the x axis.
So we draw that, in green:
The vertical asymptote is found by setting the denominator = 0
x+3 = 0
x = -3
That is the equation of a vertical line through -3 on the x axis.
So we draw that, in green:
 Since the degree of the numerator, which is 2, is greater
than the degree of the denominator, which is 1, there is
no horizontal asymptote.
Since the degree of the numerator, which is 2, is exactly 1
more than the degree of the denominator, which is 1, there
is an oblique asymptote.
The equation of the oblique asymptote is found by dividing
the denominator into the numerator by long division,
ignoring the remainder, and setting y = the quotient:
x-3
x+3)x²+0x-5
x²+3x
-3x-5
-3x-9
4
So the oblique asymptote has the equation y = x-3.
It has intercepts (3,0) and (0,-3) So we draw that
line (also in green):
Since the degree of the numerator, which is 2, is greater
than the degree of the denominator, which is 1, there is
no horizontal asymptote.
Since the degree of the numerator, which is 2, is exactly 1
more than the degree of the denominator, which is 1, there
is an oblique asymptote.
The equation of the oblique asymptote is found by dividing
the denominator into the numerator by long division,
ignoring the remainder, and setting y = the quotient:
x-3
x+3)x²+0x-5
x²+3x
-3x-5
-3x-9
4
So the oblique asymptote has the equation y = x-3.
It has intercepts (3,0) and (0,-3) So we draw that
line (also in green):
 Now we get some points (-7,-11), (-5,-10), (-4,-11), (-2,-1),
(-1,-2),(0,
Now we get some points (-7,-11), (-5,-10), (-4,-11), (-2,-1),
(-1,-2),(0,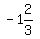 ), (1,-1), (3,
), (1,-1), (3, ), (5,
), (5, )
)
 Then draw in the graph through those points approacking the
asymptotes:
Then draw in the graph through those points approacking the
asymptotes:
 Edwin
Edwin