Question 779326: Given the endpoints of a diameter of a circle at (4,1) and (-4,-4), find the center and radius of the circle. Write its equation in standard form.
Thanks in advance for your help.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! if the endpoints of a 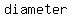 of a circle at (4,1) and (-4,-4), then the center is midpoint: of a circle at (4,1) and (-4,-4), then the center is midpoint:
 coordinate of midpoint is coordinate of midpoint is 
 coordinate of midpoint is coordinate of midpoint is 
so, the center is at ( , , ) and it means ) and it means  and and 
now find the length of radius which is equal to distance between one endpoint and midpoint of diameter
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, -1.5), we can say (x1, y1) = (0, -1.5)
So  , , 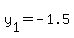
Since the second point is (4, 1), we can also say (x2, y2) = (4, 1)
So  , , 
Put this all together to get:  , , 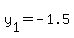 , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, -1.5) and (4, 1)

 Plug in Plug in  , , 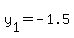 , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, -1.5) and (4, 1) is exactly 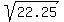 units units
The approximate distance between the two points is about 4.7169905660283 units
So again,
Exact Distance: 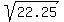 units units
Approximate Distance: 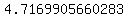 units units
|
so, radius is 
equation of a circle in standard form:




|
|
|