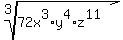Break 72 into its prime factors: 72 = 8·9 = 2³·3²
Since the index of the root is 3, write each exponent
which is not already a sum of the largest multiple of 3
as a number less than 3. That is
The exponent of 2, which is 3, is already a multiple of 3, which
is 3 itself, so leave it as is.
The exponent of 3, which is 2, is less than 3, so leave it as is.
The exponent of y, which is 4, must be written as 3+1, since 3 is
the largest multiple of 3 which does not exceed 4.
The exponent of 3, which is 11, must be written as 9+2, since 9 is
the largest multiple of 11
We know that whe we have a product of exponentials with the same base
we add the exponents, so we can reverse that principle: When we have an
exponent which is a sum, we may write it as a product of exponentials
with the same base:
So we have
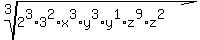Now we divide each exponent which is a multiple of 3, by the
index of the root, 3, and bring the base with the new exponent
out in front of the radical:
The 23 comes out in front as just 2
The x3 comes out in front as just x
The y3 comes out in front as just y
The z9 comes out in front as just z3
The factors with an exponent less than the index 3, remain
under the radical:
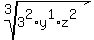Write 32 as 9 and erase the 1 exponent on the y:
Answer: 2xyz³·∛9yz²
Edwin
