SOLUTION: At the time of his son's birth, a man invests a certain sum of money at 8%, compounded quarterly, to provide quarterly payments of 60000 each for four years, the first payment to b

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: At the time of his son's birth, a man invests a certain sum of money at 8%, compounded quarterly, to provide quarterly payments of 60000 each for four years, the first payment to b      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 778287: At the time of his son's birth, a man invests a certain sum of money at 8%, compounded quarterly, to provide quarterly payments of 60000 each for four years, the first payment to be made on his son's 20th birthday. how much does the father invest?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
The problem has two parts: 1. Determine how much is needed at the beginning of the payout period to accommodate the payouts. 2. Determine what the present value of that amount is 20 years before the payouts begin.


1. Determine the principal needed to accommodate the payouts. The formula is A+=+P%2B%28P%281-%281%2Bi%29%5E%28-%28n-1%29%29%29%2Fi%29


i is the quarterly interest rate. Which is the rate divided by 4. .08/4 = .02.


P is the payout amount. $60,000


n is the number of payout periods. 16 - quarterly payments (4 per year) for 4 years.


A is the amount needed at the start of the annuity pay out period.


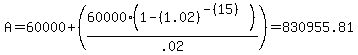
A=60000%2B%2860000%281-%281.02%29%5E%28-%2815%29%29%29%2F.02%29=830955.81


2. What is the amount he has to save now, so that it accumulates to that $830,955.81? PV = FV/(1+r)^n where r is the quarterly interest rate (.02), n is the number of quarters (20 years times 4 quarters per year = 80 quarters), and FV is the future value needed to support the annuity. That FV is 830,955.81.


PV = 830955.81/(1.02)^80 = $170,437.12