Question 777654: EAch of the two congruent sides of an isosceles triangle is 7 cm longer than half the base. Find the length of each side of the triangle.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two many triangles, with different measurements that comply with that.
Here are 3 examples:

Either you are missing some information, or you are expected to say that there are infinte solutions. If you had some other information, like the height, or one angle, you could start by
 = half the base = half the base
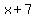 = length of the congruent sides, = length of the congruent sides,
and then use that with any extra information
IF it were a  isosceles triangle, isosceles triangle, 
then the base is the hypotenuse, with length  and the congruent sides are the legs. and the congruent sides are the legs.
Then, Pythagoras says





Flipping, and dividing both sides by 2
 --> -->  --> --> 
The solutions to that equation are

The solution with the negative sign is a negative number, which could not be the length of half the base,
so  and and  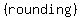
|
|
|