Question 776077: Walking at a constant speed, a person walks 3/4 of a mile every 12 min. How far does the person walk in 30 min? How long does it take the person to walk 2 1/2 miles? (cannot use cross multiplication in this problem)
Answer by josgarithmetic(39613)   (Show Source):
You can put this solution on YOUR website! Rate is 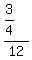 miles per minute. This is  miles per minute.
First question, let d = unknown distance in miles:
Second question, let t = unknown time in minutes:
You can solve both questions using multiplicative inverse property. Cross multiplication is not needed. The second question is more interesting, and maybe just slightly more complicated ------ but still, you only need the idea of multiplicative inverse.
Start by changing the mixed number into improper fraction:
Next, USE the multiplicative inverse of something and apply to both sides; do you know what/which to choose? You see t as a denominator. What can or do you want to do with this?
As a general example, given y is unknown, and having  , the right side contains the multiplicative inverse of y. You can use the multiplicative inverse of the multiplicative inverse of y; which is simply, y.
'
 , using multiplicative inverse of 
More steps were shown just to help see clearly the process and meaning.
|
|
|
