|
Question 775811: 4 people can paint 7 walls in 31 minutes.
How many minutes will it take for 10 people to paint 8 walls?
i need an explanation how this equals 14 9/35
thanks for your time in advance.
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1 job = 1 wall.
Look first at the 4 people doing 7 jobs in 31 minutes. One job would require these four people to only work (1/7) of the 31 minutes. Meaning is:
4 people do 1 job in (1/7)31 minutes.
WHAT is the one-person rate for 1 job? Instead of 4 people and 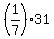 minutes, this would be 1 person and 4 times more than minutes, this would be 1 person and 4 times more than 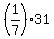 . .
1 person does at the rate of  job per minute. job per minute.
1 person rate is  job per minute. job per minute.
The uniform rate basic idea is r*t=j where r = rate of work in jobs per minute, t is the work time in minutes, and j is how much or many jobs. Also, the rates of the same kind of persons doing the work are simply added when they work together, ideally; and multiplication is used to show their count.
Given the one-person rate found, n=10 people to do the work, and j=8 for 8 walls, find t, the number of minutes to paint the 8 walls (the 8 jobs).

Solve for t.
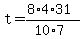

 minutes minutes
----------------------------------------------
Yes, the whole number part of the quotient IS 14.
|
|
|
| |