graph each horizontal parabola and give the domain and range:
Place them in the form
(y - k)² = 4p(x - h)
where the vertex is (h, k),
the focus is (h+p, k)
the end of the focal chord (or latus rectum) are the
points (h+p,k+2p), (h+p, k-2p)
the directrix is the vertical line whose equation
is x = h-p
the axis of symmetry is the horizontal line whose equation
is y = k
The graph opens to the right when p is positive
and to the left when p is negative.
The domain is [h, ¥) when it opens right, and
(-¥, h] when it opens left.
The range is (-¥, ¥)
1. x = y^2 + 2
Get y terms on left, other terms on right:
-y² = -x + 2
Multiply through by -1 to make left side positive
y² = x - 2
Write y as (y - 0) and x - 2 as 1(x - 2)
(y - 0)² = 1(x - 2)
Compare to
(y - k)² = 4p(x - h)
Then h = 2, k = 0, 4p = 1, p = 1/4 = .25
The vertex is (h, k) = (2, 0)
The focus is (h+p, k) = (2.25, 0)
the end of the focal chord (or latus rectum) are the
points (h+p,k+2p), (h+p, k-2p), or
(2.25, 0+2·.25) = (2.25, .5) and
(2.25, 0-2·.25) = (2.25, -.5)
the directrix is the vertical line whose equation
is x = h-p, or x = 2-.25 or x = 1.75.
the axis of symmetry is the horizontal line whose equation
is y = k, or y = 0 (the x-axis)
The graph opens to the right because p = .25 is positive
The domain is [2, ¥)
The range is (-¥, ¥)
with the directrix
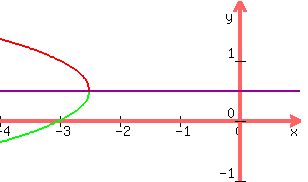
2. x = -2y^2 + 2y - 3
Get y terms on left, others right:
2y² - 2y = -x -3
Divide through by coefficient of y², which is 2
y² - y = -(1/2)x - 3/2
Add the square of 1/2 the coefficient of y to both
sides:
The coefficient of y is -1,
1/2 of -1 is -1/2.
The square of -1/2 is +1/4
y² - y + 1/4 = -(1/2)x - 3/2 + 1/4
Factor the left side, combine last two terms on
the right:
(y - 1/2)(y - 1/2) = -(1/2)x - 5/4
Write the left side as the square of a binomial,
and factor out -(1/2) on the left:
(y - 1/2)² = -1/2(x + 5/2)
or we can use decimals if we like:
(y - .5)² = -.5(x + 2.5)
Compare to
(y - k)² = 4p(x - h)
Then h = -2.5, k = .5, 4p = -.5, p = -.5/4 = -.125
The vertex is (h, k) = (-2.5, .5)
The focus is (h+p, k) = (-2.625, .5)
the end of the focal chord (or latus rectum) are the
points (h+p,k+2p), (h+p, k-2p), or
(-2.625, .5-2·(-.125) ) = (-2.625, .75) and
(-2.625, .5-2·(-.125) ) = (2.625, .25)
the directrix is the vertical line whose equation
is x = h-p, or x = -2.5-(-.125) or x = -2.375.
the axis of symmetry is the horizontal line whose equation
is y = k, or y = .5 (the x-axis)
The graph opens to the left because p = -.125 is negative
The domain is (-¥, -2.5]
The range is (-¥, ¥)
with the directrix and axis of symmetry:
3. x^2 = 1/8y
Hey, that's a vertical parabola, not a horizontal one! So it has
form
(x - h)² = 4p(y - k)
where the vertex is (h, k),
the focus is (h, k+p)
the end of the focal chord (or latus rectum) are the
points (h-2p,k+p), (h+2p, k+p)
the directrix is the horizontal line whose equation
is y = k-p
the axis of symmetry is the vertical line whose equation
is x = h
The graph opens upward when p is positive
and downward when p is negative.
Its domain is (-¥, ¥)
Its range is [k, ¥) when the parabola opens
upward and (-¥,k] when it opens downward
x^2 = 1/8y
Write x as (x-0) and y as (y-0)
(x - 0)² = 1/8(y - 0)
Compare to
(x - h)² = 4p(y - k)
Then h = 0, k = 0, 4p = 1/8, p = 1/16
where the vertex is (h, k) or (0, 0),
the focus is (0, 0+1/16) or (0, 1/16)
the end of the focal chord (or latus rectum) are the
points (h-2p,k+p), (h+2p, k+p), or
(0-2(1/16), 0+1/16) and (0+2(1/16), 0+1/16), or
(-1/8, 1/16) and (1/8, 1/16
the directrix is the horizontal line whose equation
is y = k-p or y = -1/16
the axis of symmetry is the vertical line whose equation
is x = 0 (the y-axis)
The graph opens upward because p = 1/16 which is positive.
Its domain is (-¥, ¥)
Its range is [0, ¥)
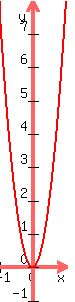with the directrix (it's the green line, and it's so
close to the x-axist that you can barely see it:
Edwin
