SOLUTION: Find the area of the triangle enclosed by the x-axis, the y-axis and the line y = 2x-6. Nice and short... but confusing! I really don't get this question!! Please help me!

Click here to see ALL problems on Triangles

Question 773946: Find the area of the triangle enclosed by the x-axis, the y-axis and the line y = 2x-6.
Nice and short... but confusing! I really don't get this question!!
Please help me!
Thanks!
Found 2 solutions by KMST, ramkikk66:
Answer by KMST(5328) (Show Source):
You can put this solution on YOUR website!
It is a right triangle with legs (the perpendicular sides) measuring 3 units and 6 units.
You can take one leg as the base and the other as the height and use
area of a triangle =

How did I draw the line?
Since the x-axis (y=0) and the y-axis (x=0) are two of the sides, I knew one vertex of the triangle was at the origin.
I needed to know the other two vertices of the triangle, which would be the points where the line crossed the axis.
Those points are the x-intercept and y-intercept.

--> --> --> tells me one vertex is at , point (3,0).

--> tells me the other vertex is at , point (0,-6).

Answer by ramkikk66(644) (Show Source):
You can put this solution on YOUR website!

The line, x axis and y axis form a right triangle, since x axis and y axis are perpendicular to each other. To find the area of the triangle, you need to know 1) the value of the x intercept (the point where the line intersects the x axis): This is the length of one side of the triangle. 2) the value of the y intercept (the point where the line intersects the y axis): This is the length of the perpendicular side of the triangle. 3) To find the x intercept, substitute y as 0 in the equation. (Why? Because the x axis is represented by the equation y = 0, and the x intercept is where the line intersects the x axis) Putting y = 0, we get 2x - 6 = 0, or x = 3. So the x intercept = (3,0) and the length of the side of the triangle is 3. 4) To find the y intercept, substitute x as 0 in the equation. (Why? Because the y axis is represented by the equation x = 0, and the y intercept is where the line intersects the y axis) Putting x = 0, we get y = 2x - 6 = -6. So the y intercept = (0,-6) and the length of the side of the triangle is 6. 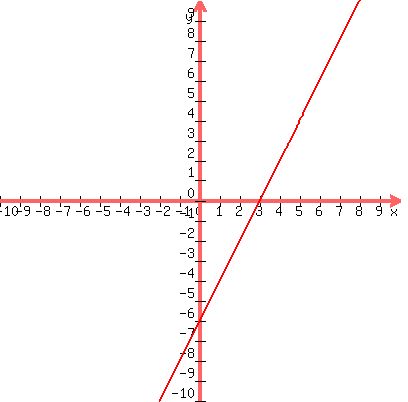5) Since we know the length of the 2 perpendicular sides of the right triangle, the area is simply The graph of the line is given below for your reference. You can clearly see the 3 vertices of the triangle are (0,0), (3,0) and (0,-6) and the lengths of the 2 perpendicular sides are 3 units and 6 units as explained above. Hope you got it :)