Question 773664: please help me answer this.... a circular garden has a radius of 15 m. if trees are to be placed around it's edge 4 m apart,how many trees are needed?
Answer by josgarithmetic(39628)   (Show Source):
You can put this solution on YOUR website! Strictly placing each tree 4 meters apart, two neighboring trees will form an isosceles triangle which includes the center point of the garden as the other point. The two equal sides are 15 meter each and as given, the base side is 4 meters.
Each such isosceles triangle has an altitude from the garden center point to the mid point of each tree-separation length; we use half of this distance,  , and the radius (same as either isosceles equal sides) to find sine of HALF the central angle.
Letting  , so  , and we want TWO TIMES this angle.
 degrees.
Central angle is repeated for each tree placement and so
 such central angles.
To be practical, the number of trees would be either 23 or 24, and would need to be a little more than 4 m or a little less than 4 m apart.
If you really wanted the trees to be 4 meters apart ALONG THE CIRCUMFERENCE of the garden, then the solution, especially the process, would be simpler to do.
MUCH SIMPLER SOLUTION (THIS SOLUTION ADDED A DAY LATER)
Four meter between each tree, and garden radius 15 m, enough to use circumference and not worry so much about angular separation.
Circumference =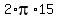 
Divide the circumference by 4 meter increments, 
_______
Again, you would choose either 23 trees, or 24 trees. One would choose the separation to be along the circumference, or according to a central angle near 15 degrees. If using 24 trees, then the distance between trees for one of them would need to be somewhat less than 4 meter while all the rest would allow the 4 m separation.
|
|
|
