To prove that:

 To prove it using induction:
1) Confirm it is true for n = 1
It is true since 1/2 = 1/2^1
2) Assume it is true for some value of n = k
i.e.
To prove it using induction:
1) Confirm it is true for n = 1
It is true since 1/2 = 1/2^1
2) Assume it is true for some value of n = k
i.e.

 ----> eqn (1)
3) Now prove it is true for n = k+1
i.e. the sum up to (k+1) terms = 1 - 1/2^(k+1)
Proof:
For n = k+1, the expression of the sum is:
----> eqn (1)
3) Now prove it is true for n = k+1
i.e. the sum up to (k+1) terms = 1 - 1/2^(k+1)
Proof:
For n = k+1, the expression of the sum is:

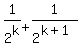 =
=
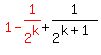 ---> from eqn(1)
=
---> from eqn(1)
=
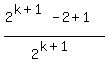 ---> taking common denominator 2^(k+1)
=
---> taking common denominator 2^(k+1)
=
 ---> simplifying the numerator
=
---> simplifying the numerator
=
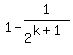 Proved!
4) So we have proved that if the formula is true for n=k, it is true for
n=k+1. Since it is true for n=1, it is proved by mathematical induction, that
it is true for all n.
Hope you got it :)
Proved!
4) So we have proved that if the formula is true for n=k, it is true for
n=k+1. Since it is true for n=1, it is proved by mathematical induction, that
it is true for all n.
Hope you got it :)