Let the parking hours be x per month, and the fee be y.
In the first case, fee is fixed and not dependent on number of hours.
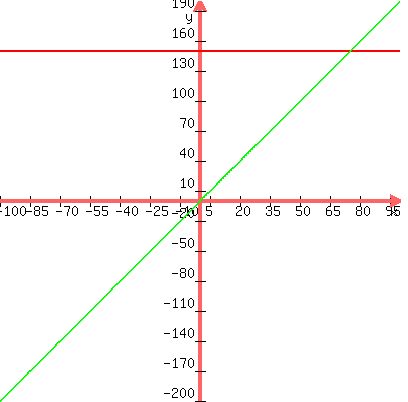
i.e. y is independent of x. The equation in this case is y = 150.
In the second case, the fee is $2 per hour. Or the equation is y = 2*x.
Taking the two equations
----> (1)
----> (2)
They intersect at a point where 2*x = 150 or x = 75.
Obviously, if the parking hours > 75, he has to pay a fee of more than the flat
fee of 150. Since he needs 160 hours of parking per month, the first option of
$150 is clearly better. Option 2 is better only if he is parking for < 75 hours
per month.
Hope you got it :) See the graph below.
(