Question 77304: Solve the following word problem.
The hypotenuse of a right triangle is four feet longer than three times the shorter leg. The longer leg is one foot less than the hypotenuse. Find the dimensions of the right triangle.
Found 2 solutions by jim_thompson5910, checkley75:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let a=shorter leg, b=longer leg, c=hypotenuse
So we have
 "The hypotenuse of a right triangle is four feet longer than three times the shorter leg" "The hypotenuse of a right triangle is four feet longer than three times the shorter leg"
 "The longer leg is one foot less than the hypotenuse" "The longer leg is one foot less than the hypotenuse"
Now solve for a:



Plug 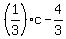 into a and plug in into a and plug in 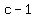 into b of the Pythagorean theorem into b of the Pythagorean theorem

 foil the terms on the left side foil the terms on the left side
 Combine like terms Combine like terms
 Subtract Subtract  from both sides from both sides
Now use the quadratic formula to solve for c (note:this solver uses decimals instead of fractions):
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=7.11111111111112 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 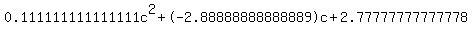 can be factored: can be factored:

Again, the answer is: 25, 1.
Here's your graph:
 |
So the hypotenuse is:
c=1 or c=25
Use this to find a
Let c=1


Since this length is negative, we must disregard the hypotenuse length of 1
Let c=25


Now use c=25 to find b


So our dimensions are:
a=7,b=24,c=25
Check:
 Plug in a=7, b=24, c=25 Plug in a=7, b=24, c=25


 works works
 plug in a=7 and c=25 plug in a=7 and c=25

 works works


 works works
Answer by checkley75(3666)   (Show Source): (Show Source):
You can put this solution on YOUR website! HYP=(3X+4) X BEING THE SHORTEST LEG1.
LONGER LEG2=(3X+4)-1
THUS THE HYP^2=(LEG1)^2+(LEG*2)^2
(3X+4)^2=X^2+(3X+4-1)^2
9X^2+24X+16=X^2+(3X+3)^2
9X^2+24X+16=X^2+9X^2+18X+9 WE CAN CANCEL OUT THE 9X^2 TERMS & WE HAVE LEFT
24X-X^2-18X+16-9=0
-X^2+6X+7=0
X^2-6X-7=0
(X-7)(X+1)=0
X-7=0
X=7 ANSWER.
HYP=3*7+4
HYP=21+4
HYP=25 ANSWER.
LONG SIDE=(3*7+3)
LONG SIDE=24 ANSWER.
SHORT SIDE=7 ANSWER.
25^2=24^2+7^2
625=576+49
625=625
|
|
|