Question 771999: Hello. My name is Joanne. Can you please help me solve this problem?
A mother wants to invest $14000 for her son's future education. She invests a portion of the money in a bank certificate of deposit (CD) which earns 4% and the remainder in a savings bond that earns 7%. If the total interest earned after one year is $840, how much moves was invested in the CD?
The answer is $4666.67.
I tried using the formula, A=(1+r/n)^nt, but I am not sure if this is the correct formula to use. Also, I am not sure how to plug in the variables in the formula.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hello. My name is Joanne. Can you please help me solve this problem?
A mother wants to invest $14000 for her son's future education. She invests a portion of the money in a bank certificate of deposit (CD) which earns 4% and the remainder in a savings bond that earns 7%. If the total interest earned after one year is $840, how much moves was invested in the CD?
The answer is $4666.67.
I tried using the formula, A=(1+r/n)^nt, but I am not sure if this is the correct formula to use. Also, I am not sure how to plug in the variables in the formula.
You don’t need the future value formula  for this problem, as you’re not calculating TVM (time value of money), or the value of the $14,000 over a certain time period. You’re just trying to determine how much of the $14,000 was invested in the CD. for this problem, as you’re not calculating TVM (time value of money), or the value of the $14,000 over a certain time period. You’re just trying to determine how much of the $14,000 was invested in the CD.
As a result, you just simply do the following:
Let amount invested in CD be C
Then amount invested in savings bond = 14,000 – C
Amount of interest earned on the CD, at a 4% interest rate = .04(C), or .04C
Amount of interest earned on the savings bond, at a 7% interest rate = .07(14,000 – C)
Amount of interest earned on CD, plus amount of interest earned on savings bond, equals total interest earned, OR
.04C + .07(14,000 – C) = 840
.04C + 980 - .07C = 840
.04C - .07C = 840 – 980
- .03C = - 140
C, or amount invested in CD = 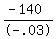 , or $ , or $
You can do the check!!
Further help is available, online or in-person, for a fee, obviously. Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com
|
|
|