SOLUTION: how to find exact value of sin(cos^-1(-1/3))

sin[cos-1()]

First we find the angle cos-1()

The inverse cosine of a negative number is in quadrant II
between 90° or  and 180° or p.

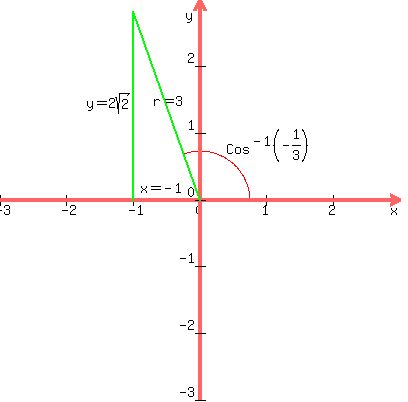
We'll draw the picture of the angle cos-1() in quadrant
II.

Since the cosine is 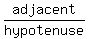 =  we take x
as the numerator of 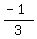, x=-1, and the r as the denominator,
3, r=3:



Then we calculate y by the Pythagorean theorem 

   x² + y² = r²
(-1)² + y² = 3²
    1 + y² = 9
        y² = 8
         y = √8
         y = √4·2
         y = 2√2



Therefore sin[cos-1()] =  =  = .   

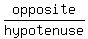Edwin