|x-1| + |x-2| + |x-4| ≧ 6
There are 8 cases to consider
1. x-1 ≧ 0, x-2 ≧ 0, and x-4 ≧ 0
2. x-1 ≧ 0, x-2 ≧ 0, and x-4 ≦ 0
3. x-1 ≧ 0, x-2 ≦ 0, and x-4 ≧ 0
4. x-1 ≧ 0, x-2 ≦ 0, and x-4 ≦ 0
5. x-1 ≦ 0, x-2 ≧ 0, and x-4 ≦ 0
6. x-1 ≦ 0, x-2 ≧ 0, and x-4 ≦ 0
7. x-1 ≦ 0, x-2 ≦ 0, and x-4 ≧ 0
8. x-1 ≦ 0, x-2 ≦ 0, and x-4 ≦ 0
They simplify to
1. x ≧ 1, x ≧ 2, and x ≧ 4 ↠ x ≧ 4
2. x ≧ 1, x ≧ 2, and x ≦ 4 ↠ 2 ≦ x ≦ 4
3. x ≧ 1, x ≦ 2, and x ≧ 4 ↠ contradiction
4. x ≧ 1, x ≦ 2, and x ≦ 4 ↠ 1 ≦ x ≦ 2
5. x ≦ 1, x ≧ 2, and x ≦ 4 ↠ contradiction
6. x ≦ 1, x ≧ 2, and x ≦ 4 ↠ contradiction
7. x ≦ 1, x ≦ 2, and x ≧ 4 ↠ contradiction
8. x ≦ 3, x ≦ 2, and x ≦ 4 ↠ x ≦ 2
Four of those are obviously contradictions
So we have only four cases to consider:
1. x ≧ 1, x ≧ 2, and x ≧ 4 ↠ x ≧ 4
2. x ≧ 1, x ≧ 2, and x ≦ 4 ↠ 2 ≦ x ≦ 4
4. x ≧ 1, x ≦ 2, and x ≦ 4 ↠ 1 ≦ x ≦ 2
8. x ≦ 3, x ≦ 2, and x ≦ 4 ↠ x ≦ 2
Case 1: x ≧ 1, x ≧ 2, and x ≧ 4 ↠ x ≧ 4
1. x-1 ≧ 0, x-2 ≧ 0, and x-4 ≧ 0
|x-1| + |x-2| + |x-4| ≧ 6
becomes:
x-1 + x-2 + x-4 ≧ 6
3x-7 ≧ 6
3x ≧ 13
x ≧ 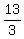 Case 2: x ≧ 1, x ≧ 2, and x ≦ 4 ↠ 2 ≦ x ≦ 4
2. x-1 ≧ 0, x-2 ≧ 0, and x-4 ≦ 0
|x-1| + |x-2| + |x-4| ≧ 6
becomes:
x-1 + x-2 - x+4 ≧ 6
x+1 ≧ 6
x ≧ 5
That contradicts x ≦ 4 so case 2 is eliminated
Case 4: x-1 ≧ 0, x-2 ≦ 0, and x-4 ≦ 0
4. x ≧ 1, x ≦ 2, and x ≦ 4 ↠ 1 ≦ x ≦ 2
|x-1| + |x-2| + |x-4| ≧ 6
beomes:
x-1 - x+2 - x+4 ≧ 6
-x+6 ≧ 6
-x ≧ 0
x ≦ 0
That contradicts x ≧ 1 so case 4 is eliminated
Case 8: x-1 ≦ 0, x-2 ≦ 0, and x-4 ≦ 0
4. x ≦ 1, x ≦ 2, and x ≦ 4 ↠ x ≦ 1
|x-1| + |x-2| + |x-4| ≧ 6
becomes:
-x+1 - x+2 - x+4 ≧ 6
-3x+7 ≧ 6
-3x ≧ -1
x ≦
Case 2: x ≧ 1, x ≧ 2, and x ≦ 4 ↠ 2 ≦ x ≦ 4
2. x-1 ≧ 0, x-2 ≧ 0, and x-4 ≦ 0
|x-1| + |x-2| + |x-4| ≧ 6
becomes:
x-1 + x-2 - x+4 ≧ 6
x+1 ≧ 6
x ≧ 5
That contradicts x ≦ 4 so case 2 is eliminated
Case 4: x-1 ≧ 0, x-2 ≦ 0, and x-4 ≦ 0
4. x ≧ 1, x ≦ 2, and x ≦ 4 ↠ 1 ≦ x ≦ 2
|x-1| + |x-2| + |x-4| ≧ 6
beomes:
x-1 - x+2 - x+4 ≧ 6
-x+6 ≧ 6
-x ≧ 0
x ≦ 0
That contradicts x ≧ 1 so case 4 is eliminated
Case 8: x-1 ≦ 0, x-2 ≦ 0, and x-4 ≦ 0
4. x ≦ 1, x ≦ 2, and x ≦ 4 ↠ x ≦ 1
|x-1| + |x-2| + |x-4| ≧ 6
becomes:
-x+1 - x+2 - x+4 ≧ 6
-3x+7 ≧ 6
-3x ≧ -1
x ≦  So the two cases that aren't self- contradictory are
cases 1 and 8. So the original inequality is true when
x ≦
So the two cases that aren't self- contradictory are
cases 1 and 8. So the original inequality is true when
x ≦  or when x ≧
or when x ≧ 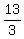 The solution is the union of the solutions for those two cases:
(-∞,
The solution is the union of the solutions for those two cases:
(-∞, ) U (
) U (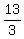 ,∞)
Edwin
,∞)
Edwin