We must get the circle in standard form:
(x - h)² + (y - k)² = r²
in order to get the radius.
4x² + 4y² - 7x + 6y - 35 = 0
4x² - 7x + 4y² + 6y = 35
Divide through by 4
x² -  x + y² +
x + y² +  y =
y =  x² -
x² -  x + y² +
x + y² +  y =
y =  (x² -
(x² -  x) + (y² +
x) + (y² +  y) =
y) =  Complete the square in each parentheses)
For the first parentheses:
Multiply the coefficient of x, which is
Complete the square in each parentheses)
For the first parentheses:
Multiply the coefficient of x, which is 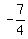 by
by  ,
getting
,
getting  , then square that
, then square that 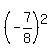 =
= 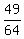 Add that in the first parentheses and also add it to the right side.
For the second parentheses:
Multiply the coefficient of y, which is
Add that in the first parentheses and also add it to the right side.
For the second parentheses:
Multiply the coefficient of y, which is  by
by  ,
getting
,
getting  , then square that
, then square that  =
=  Add that in the second parentheses and also add it to the right side.
(x² -
Add that in the second parentheses and also add it to the right side.
(x² -  x +
x + 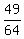 ) + (y² +
) + (y² +  y +
y +  ) =
) =  +
+ 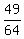 +
+  Factor each parentheses
(x -
Factor each parentheses
(x -  )² + (y -
)² + (y -  ) =
) =  +
+ 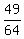 +
+  Get a LCD of 64 for the fractions on the right side:
Get a LCD of 64 for the fractions on the right side:
 +
+ 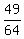 +
+  =
= 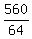 +
+ 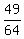 +
+ 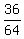 =
= 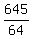 So the center is (
So the center is ( ,
,  ) and the radius is
) and the radius is 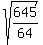 =
= 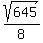 . That wasn't necessary because we only need
r²=
. That wasn't necessary because we only need
r²= 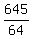 to find the area.
The area is
A = pr² = p(
to find the area.
The area is
A = pr² = p(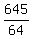 ) =
) =  which is approximately 31.66 square units.
which is approximately 31.66 square units.
 Edwin
Edwin