Question 771401: Line A has a slope of -4 and passes through (-25,-10). line B has x intercept of 10 and y intercept of 25.
a.)the distance of line A to point (8,-3).
b.)the point of intersection of lines A and B.
c.)determine the equation of the line perpendicular to line B and passing through (-20,10).
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Using some general point on a line, (u,v), the the point-slope form of a line would be  , from which you can make 
Using that general point-slope formula for a line, you find line A this way:
 ________________Line A.
You can do similarly for line B.
Question (a): How far is line A to (8, -3)?
The best way to start this one is, find the line containing (8, -3) which is perpendicular to line A. In finding this, initially we do not know the y-intercept.
We want slope  .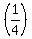
 where unknown y-intercept is b.
This perpendicular line to A is  .
What is intersection point of  and  ?
Equating the y formulas, solving for x, then returning and solving for y,
these line intersect at.... (-420/17, 20/17).
Use distance formula to find the distance from (-420/17, 20/17) to (8, -3).
Remaining calculation not shown...)
|
|
|
