SOLUTION: Can the following equation be solved using only algebra? log base 2 of (6x-8) = log base 3 of (20x+1) The TI-83 gives the solution x = 4 which checks. Graphing the equatio

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Can the following equation be solved using only algebra? log base 2 of (6x-8) = log base 3 of (20x+1) The TI-83 gives the solution x = 4 which checks. Graphing the equatio      Log On


   

Question 771261: Can the following equation be solved using only algebra?
log base 2 of (6x-8) = log base 3 of (20x+1)
The TI-83 gives the solution x = 4 which checks.
Graphing the equations y = log base 2 of (6x-8) and y = log base 3 of (20x+1) gives a solution of x = 4.
Can this equation be solved with algebra only?
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Can the following equation be solved using only algebra?
log base 2 of (6x-8) = log base 3 of (20x+1)
The TI-83 gives the solution x = 4 which checks.
Graphing the equations y = log base 2 of (6x-8) and y = log base 3 of (20x+1) gives a solution of x = 4.
Can this equation be solved with algebra only?
===================
No, it can't.
Only numerical or graphical methods work.
------

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The other tutor, Alan, is right about your equation.

The bases 2 and 3 are not powers of the same number. 

However equations of the form 

logA(Bx+C) = logD(Ex+F)

can be solved algebraically if the bases are 
powers of the same integer, such as this equation,

log4(2x-1) = log8(7x-8)

This is solvable by algebraic methods:

Let both sides equal to K

log4(2x-1) = K  and  log8(7x-8) = K

4K = 2x-1       and  8K = 7x-8

(22)K = 2x-1     and  (23)K = 7x-8

22K = 2x-1       and  23K = 7x-8

Raise both sides of the first equation to the 3rd power and both sides
of the second equation to the 2nd power.

(22K)3 = (2x-1)3     and  (23K)2 = (7x-8)2

26K = (2x-1)3     and  26K = (7x-8)2

Now we can equate the rights sides since both equal26K

(2x-1)3 = (7x-8)2

   8x³ - 12x² + 6x - 1 = 49x²- 112x + 64

8x³ - 61x² + 118x - 65 = 0

Find possible rational zeros. 

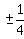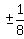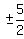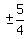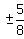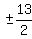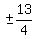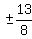±1, %22%22+%2B-+1%2F2, %22%22+%2B-+1%2F4, %22%22+%2B-+1%2F8, ±5, %22%22+%2B-+5%2F2, %22%22+%2B-+5%2F4, %22%22+%2B-+5%2F8, ±13, %22%22+%2B-+13%2F2, %22%22+%2B-+13%2F4, %22%22+%2B-+13%2F8, ±65  

Try 1 with synthetic division:

1 | 8  -61   118  -65
  |      8   -53   65
    8  -53    65    0

So we have factored the equation as

(x-1)(8x²-53x+65) = 0

And the quadratic factors as

(x-1)(x-5)(8x-13) = 0

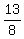x = 1, x = 5, and x = 13%2F8

So there are three answers, but we must check
to see if any are extraneous.  1 does not
check because it causes 7x-8 to be negative.
The other two solutions check.
So there are two solutions: 

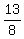x = 5, and x = 13%2F8

But that was solvable only because the bases were both
powers of 2.
  | 
Edwin