SOLUTION: Hello, is anybody able to explain: WHY solutions of the quadratic equation y=7x^2-3x-11 (has two solutions because the discriminant is positive) are irrational?

Algebra ->  Equations -> SOLUTION: Hello, is anybody able to explain: WHY solutions of the quadratic equation y=7x^2-3x-11 (has two solutions because the discriminant is positive) are irrational?       Log On


   

Question 771214: Hello, is anybody able to explain:
WHY solutions of the quadratic equation y=7x^2-3x-11 (has two solutions because the discriminant is positive) are irrational?
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
The possibility of irrational solutions when y=0 is because x has been squared. The solution process must take a step from a squared term, yielding the square root of the square expression.
You might start with something represented like %28x%2Bp%29%5E2=V, and you want to know what is x. Raise both sides to the power of %281%2F2%29 and you have:
x%2Bp=%2Bsqrt%28V%29 or x%2Bp=-sqrt%28V%29.
You need both the plus and the minus because either, when or if squared again, will become 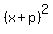%28x%2Bp%29%5E2 in its positive form (without showing any negative sign with x+p).

Continuing from there,
x=-p%2Bsqrt%28V%29 or x=-p-sqrt%28V%29.
V can possibly be not a perfect square, so x will be the two irrational solutions. In case V is actually a perfect square, then naturally, the solutions for x would be rational.


At the middle of your question, you showed the example equation y=7x%5E2-3x-11. Try setting y=0 and complete the square to solve for x. You may see how this works and that you will have two irrational solutions for x. We can check the discriminant now, yet before you try to solve for x:
%28-3%29%5E2-4%2A%287%29%2A%28-11%29=9%2B7%2A44=317, A POSITIVE VALUE. TWO REAL SOLUTIONS, and because 317 is NOT a perfect square, the solutions for x will be irrational.