SOLUTION: For the equation x - 2SQRT of X=0 , perform the following: a) Solve for all values of x that satisfies the equation. b) Graph the functions y = x and y=2 SQRT of X on

For the equation  , 
perform the following:
a) Solve for all values of x that 
satisfies the equation. 



Isolate the radical term by adding 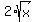 to both sides

 

Square both sides





Get 0 on the right



Factor x out on the left



Use the zero-factor property
and set each of the factors
x and x-4 equal to 0.

 gives answer as 0
 gives another answer as 4

We must check these in the original





So 0 checks





(((0=0)))
So 4 checks too.

b) Graph the functions y = x and 
y=2 SQRT of X on the same graph (by plotting 
points if necessary). Show the points of 
intersection of these two graphs.

The idea here is to take the equation
 and set y = to each side.
Then graph the two equations. Then the two 
values of y should be equal when the two sides 
of  are equal, and that
will be where the graphs intersect.

Some points on  are 
(-2,-2), (-1,-1) (2,2) (5,5)

Some points on  are 
(.5,1.4), (1,2), (3,3.5), (5,4.5)



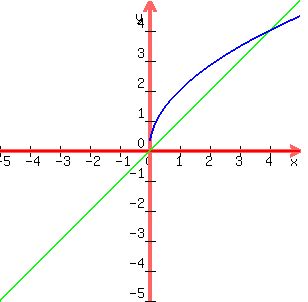So we see that the blue curve and the green 
line intersect at (0,0) and (4,4) and the 
x-values are 0 and 4 at those points, which 
correspond to the algebraic solution for x 
above.

Edwin