Question 77052: Use the factor theorem to show that if 2^p - 1, where p does not equal 3, is a prime number, then p is neither divisible by 4 nor divisible by 3. (Alternatively, prove that if p is divisible by 4 or 3, then 2^p - 1 is divisible by some number other than positive/negative itself or positive/negative 1.)
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! We use the factor theorem, which is the identity:
 ( ( + иии + + иии +  + иии + + иии +  )
Suppose p is divisible by 4, then there exists
positive integer q such that p=4q, then )
Suppose p is divisible by 4, then there exists
positive integer q such that p=4q, then
 = =
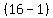 ( (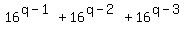 + иии + + иии + 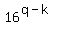 + иии + + иии +  ) =
15( ) =
15(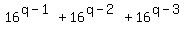 + иии + + иии + 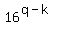 + иии + + иии +  ) so ) so
 is either 15 (when q=1) or divisible
by 15, and in either case is not prime.
For the case when p is divisible by 3, then there exists
positive integer q such that p=3q. Do the same as
above and you have 7 where the 15 is above and is either 15 (when q=1) or divisible
by 15, and in either case is not prime.
For the case when p is divisible by 3, then there exists
positive integer q such that p=3q. Do the same as
above and you have 7 where the 15 is above and  is not prime unless it equals 7, i.e., unless q=1, i.e.,
unless p=3, but that is ruled out in the hypothesis.
Edwin
is not prime unless it equals 7, i.e., unless q=1, i.e.,
unless p=3, but that is ruled out in the hypothesis.
Edwin
|
|
|