Question 770511: Divide using long division (21x^3-7)(3x-1)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Division is done differently in different countries, meaning that the numbers and expressions are arranged on the paper in different configurations.
If the way you are expected to arrange the various expressions is not the same, you may still get the idea.
I learned the American way when my children were in school, and I thought it made more sense than the way I had learned it myself, a long, long time ago, in a country far, far away.
This is how I believe an American would write it:
Write the polynomial to be divided, including zero terms, to the write under the division symbol, separated from the divisor, 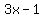 , which placed to the left:
Estimate the first term of the quotient by dividing first terms,  and wirte it above the first term of the polynomial being divided.
Then, multiply that result times the divisor,  , and subtract it from the polynomial being divided:
The result is a partial remainder. Add to that the next term of the polynomial being divided, and repeat the procedure to find the next term of the quotient and another partial remainder:
Repeat the step above one more time to find the last term of the quotient and the final remainder:
|
|
|
