In order to factor 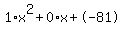 , first we need to ask ourselves: What two numbers multiply to -81 and add to 0? Lets find out by listing all of the possible factors of -81 , first we need to ask ourselves: What two numbers multiply to -81 and add to 0? Lets find out by listing all of the possible factors of -81
Factors:
1,3,9,27,81,
-1,-3,-9,-27,-81,List the negative factors as well. This will allow us to find all possible combinations
These factors pair up to multiply to -81.
(-1)*(81)=-81
(-3)*(27)=-81
(-9)*(9)=-81
Now which of these pairs add to 0? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 0
| First Number | | | Second Number | | | Sum | | 1 | | | -81 | || | 1+(-81)=-80 | | 3 | | | -27 | || | 3+(-27)=-24 | | 9 | | | -9 | || | 9+(-9)=0 | | -1 | | | 81 | || | (-1)+81=80 | | -3 | | | 27 | || | (-3)+27=24 | | -9 | | | 9 | || | (-9)+9=0 | We can see from the table that -9 and 9 add to 0.So the two numbers that multiply to -81 and add to 0 are: -9 and 9
Now we substitute these numbers into a and b of the general equation of a product of linear factors which is:
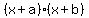 substitute a=-9 and b=9
So the equation becomes:
(x-9)(x+9)
Notice that if we foil (x-9)(x+9) we get the quadratic substitute a=-9 and b=9
So the equation becomes:
(x-9)(x+9)
Notice that if we foil (x-9)(x+9) we get the quadratic 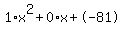 again again
Now replace the x's with n's to get:

Set each factor equal to zero:





So our answer is:
 or or  or or 
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
.
Notice that both terms on the left side contain the common factor n. Factor it out to
get:
.

.
Next notice that the expression within the parentheses is in the form of the difference
of two squares. This is a common form that can be factored according to the following
rule:
.

.
Applying this rule to  results in the factors results in the factors 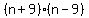 . Substituting this . Substituting this
into our first factor changes it to:
.

.
This equation will be true if any of the three factors on the left side equal zero. Therefore,
set each of the factors equal to zero and solve for the corresponding value of n, and the
resulting three values of n will make the equation correct.
.
First, let  . No solving is necessary. This tells you immediately one value of n . No solving is necessary. This tells you immediately one value of n
that will cause the original equation of  to become 0 = 0. to become 0 = 0.
.
Next, let  . Subtract 9 from both sides of the equation, and the resulting . Subtract 9 from both sides of the equation, and the resulting
equation is  . This tells you that if you let n = -9 in the original equation, . This tells you that if you let n = -9 in the original equation,
the original equation of  will become 0 = 0. will become 0 = 0.
.
Finally, let  . Add 9 to both sides of this equation and the resulting . Add 9 to both sides of this equation and the resulting
equation is  . If you let n = +9 in the original equation, the original equation . If you let n = +9 in the original equation, the original equation
of  will become 0 = 0. will become 0 = 0.
.
So the solutions to the original problem are n = 0, n = -9, and n= +9.
.
Hope this helps and shows you a way that you can solve for equations that can be factored.
|
|