1.Find the equation of a hyperbola which has the foci of the ellipse 4x^2+9y^2=36 as vertices and the vertices of the ellipse as foci. sktch the graph.
4x² + 9y² = 36
Divide through by 36
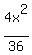
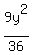
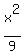
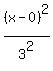
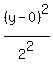
That is of the form
So the ellipse has center (0,0), a=3, so the vertices are (3,0),
b = 2, so covertices are (0,±2)
The distance from center to focis is c, and c² = a²-b², so we calculate c
c² = a²-b²
c² = 3²-2²
c² = 9-4
c² = 5
c = √5
Here is that ellipse:
The hyperbola has equation of the form
center (0,0), vertices (±√5,0), and foci (±3,0). To find b, we use this equation:
c² a² + b²
3² = (±√5)² + b²
9 = 5 + b²
4 = b²
2 = b
So the hyperbola equation is
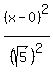
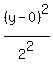
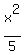
Here is the hyperbola:
-------------------------------
2.Two members of the family of circles have radii all equal to 2 units, and are centred at (-2,2, and (2,-2)respectively.Find a member of this family that passes through the point (2,2). Sketch the graph.
If this means all the circles with radii =2, then there are an infinite number
of circles with radius = 2
Choose any center which is 2 units from the point (2,2), soch as
(4,2), (2,4), (0,2), (2,0). They are the four green circles below:
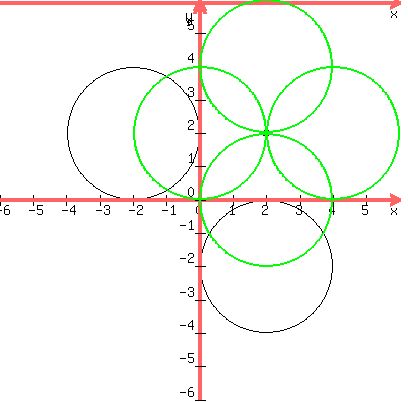The one centered at (4,2) has equation (x-4)²+(y-2)²=4
The one centered at (2,4) has equation (x-2)²+(y-4)²=4
The one centered at (0,2) has equation x²+(y-2)²=4
The one centered at (2,0) has equation (x-2)²+y²=4
Edwin
