Question 770123: How to solve this problem please: At the beginning of a bicycle ride for charity, Yady Saldarriaga and Dane McGuckian are 30 mi. apart. If they leave at the same time and ride in the same direction, Yady overtakes DAne in 6 hours. If they ride toward each other, they pass each other in 1 hr. What are their rates?
Found 2 solutions by Edwin McCravy, stanbon:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! How to solve this problem please: At the beginning of a bicycle ride for charity, Yady Saldarriaga and Dane McGuckian are 30 mi. apart. If they leave at the same time and ride in the same direction, Yady overtakes DAne in 6 hours. If they ride toward each other, they pass each other in 1 hr. What are their rates?
Let the speed of the faster bike be x mi/hr
Let the speed of the slower bike be y mi/hr
Whether the faster catches up to the slower when they are going in the same
direction, or whether they ride toward each other and meet, the 30 mile
distance between them shinks to zero.
When traveling in the same direction the catch-up rate of the faster bike
to the slower bike is at a speed of x-y.
Since time =  , the faster catches up the entire 30 miles
head start which the slower one has on the faster in , the faster catches up the entire 30 miles
head start which the slower one has on the faster in 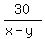 hours.
That is, the 30 miles between them shrinks to zero (by the faster catching up)
in hours.
That is, the 30 miles between them shrinks to zero (by the faster catching up)
in
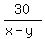 hours, and we are given that that is 6 hours. So we have the equation
hours, and we are given that that is 6 hours. So we have the equation
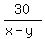 = 6
When traveling in opposite directions they approach each other at the speed
x+y.
Since time = = 6
When traveling in opposite directions they approach each other at the speed
x+y.
Since time =  , the 30 miles between them shrinks to zero (by them
meeting each other) in , the 30 miles between them shrinks to zero (by them
meeting each other) in 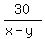 hours, and we are given that that is 1 hour.
So we have the equation hours, and we are given that that is 1 hour.
So we have the equation
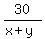 = 1
And so we have the system of equations: = 1
And so we have the system of equations:
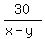 = 6 = 6
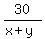 = 1
Clearing the first equation of fractions, we have:
30 = 6(x-y)
30 = 6x - 6y
Divide through by 6
5 = x - y
Clearing the second equation of fractions, we have:
30 = 1(x+y)
30 = x + y
Now the system is
5 = x - y
30 = x + y
Adding the two equations term by term, we have:
35 = 2x
Dividing both sides by 2, we have:
17.5 = x
So the faster bike goes at 17.5 mi/hr.
Substituting 17.5 for x in
5 = x - y
5 = 17.5 - y
y = 12.5
So the slower bike goes at 12.5 mi/hr.
Edwin = 1
Clearing the first equation of fractions, we have:
30 = 6(x-y)
30 = 6x - 6y
Divide through by 6
5 = x - y
Clearing the second equation of fractions, we have:
30 = 1(x+y)
30 = x + y
Now the system is
5 = x - y
30 = x + y
Adding the two equations term by term, we have:
35 = 2x
Dividing both sides by 2, we have:
17.5 = x
So the faster bike goes at 17.5 mi/hr.
Substituting 17.5 for x in
5 = x - y
5 = 17.5 - y
y = 12.5
So the slower bike goes at 12.5 mi/hr.
Edwin
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! At the beginning of a bicycle ride for charity, Yady Saldarriaga and Dane McGuckian are 30 mi. apart. If they leave at the same time and ride in the same direction, Yady overtakes DAne in 6 hours. If they ride toward each other, they pass each other in 1 hr. What are their rates?
-------
Same direction DATA:
=====================
Dane distance = x miles ; time = 6 hrs ;rate = x/6 mph
Yady distance = x + 30 mile ; time = 6 hrs ; rate = (x+30)/6 mph
---------
Toward each other Equation:
x/6 + (x+30)/6 = 30
x + x+30 = 180
2x = 150
x = 75 miles
----
Dane rate = 75/6 = 25/2 = 12.5 mph
Yady rate = (75+30)/6 = 105/6 = 17.5 mph
----------------
Cheers,
Stan H.
==================
|
|
|