Question 768965: here is the equation
7^2 + 24^2 = c^2
find
Sin = Opposite/hypotenuse
Cos = adjacent/hypotenuse
Tangent = opposite /adjacent
cotangent = adjacent/opposite
secant = hypotenuse/adjacent
cosecant = hypotenuse /opposite.
thank you
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!
Since you don't specify which of the two legs is the "opposite" and which is the "adjacent", I can't actually do this problem. But I'll tell you what you need to do:
First do the arithmetic to determine the value of 
Then take the positive square root of to determine the value of  , which is the hypotenuse.
Then, once you decide which leg, that is 7 or 24, is the opposite, and which is the adjacent, that is, 24 or 7, just do the indicated divisions.
John
Egw to Beta kai to Sigma
My calculator said it, I believe it, that settles it
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
7² + 24² = c² compare that equation to the Pythagorean theorem:
a² + b² = c²
So a = 7, b = 24,
c² = 7² + 24² = 49 + 576 = 625
c = √625
c = 25
That suggests this right triangle:
Capital letters A.B, and C indicate the three angles,
Small letters a,b, and c represent the three sides
opposite the corresponding angles.
The side "a" is the side opposite (across the triangle) from angle "A"
The side "b" is the side opposite (across the triangle) from angle "B"
The side "c" is the side opposite (across the triangle) from angle "C"
The angle "C" is normally chosen as the 90° angle in a right triangle.
The longest side "c", which is opposite the right angle C is called the
"hypotenuse"
The side "a" is the side adjacent (next to) the acute angle B
The side "b" is the side adjacent (next to) the acute angle A
As the other tutor mentioned, you didn't tell which angle to find the
trigonometric ratios of, so I'll do both. The abbreviations for the
six trig ratios are
sine = sin( )
cosine = cos( )
tangent tan( )
cotangent = cot( )
secant = sec( )
cosecant = csc( )
and you must always put the angle in parentheses to indicate
which angle you are talking about.
If you are talking about acute angle A then
sin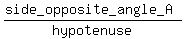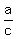(A) =  =  = 
cos(A) =  =  =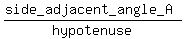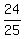 
tan(A) =  =  = 
cot(A) =  =  =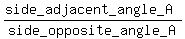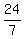 
sec(A) =  =  = 
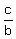csc(A) =  =  = 
If you are talking about acute angle B then
sin(B) =  = =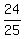
cos(B) =  = =
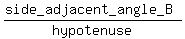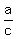tan(A) =  = =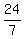
cot(B) =  = =
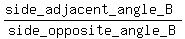sec(B) =  = =
csc(B) =  = =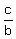
Notice the Cofunction identities:
sin(A)=cos(B), cos(A)=sin(B), tan(A)=cot(B),
cot(A)=tan(B), sec(A)=csc(B), csc(A)=sec(B)
Notice the Reciprocal identities:
 ,  ,  ,  ,  , 
 ,  ,  ,  ,  , 
Edwin
|
|
|
