Question 768603: Find the greatest number of 6 digit dividing by 15,18,21,24,27 leaves the remainder 10,13,16,19,and 22.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The remainders are always 5 short of the divisor.
For example, if the number,  is divided by 15, the remainder is is divided by 15, the remainder is  , so that for some integer , so that for some integer  , ,
 --> --> , ,
which makes 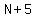 a multiple of a multiple of  . .
The same happens with 18, 21, 24, and 27.
That number,  , is such that , is such that 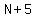 is a multiple of 15, 18, 21, 24, and 27. is a multiple of 15, 18, 21, 24, and 27.
That means 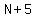 is a multiple of the least common multiple of is a multiple of the least common multiple of
 , ,
 , ,
 , ,
 , and , and
 , ,
and that least common multiple is

Dividing 1,000,000 by 7560 we find a quotient of 132 plus a remainder of 2080.
That means that  --> -->
and 997,920 is a multiple of 7560.
The next multiple of 7560 is 
That means that 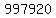 is the largest is the largest 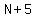 multiple of 15, 18, 21, 24, and 27 that will yield a number multiple of 15, 18, 21, 24, and 27 that will yield a number  with 6 digits, with 6 digits,
So  --> -->  . .
|
|
|