Question 7686: what is the absolute value for this problem? 2r + 9 > 19 The 2r + 9 is in absolute equations marks, my computer does not have those symbols.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! |2r+9| > 19 Remove the absolute-value bars and write the two inequalities:
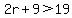 and and  Solve these inequalities: Add 9 to both sides of each. Solve these inequalities: Add 9 to both sides of each.
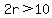 and and 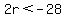 Divide both sides of each by 2. Divide both sides of each by 2.
 and and 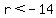
If you are wondering why you have two inequalities when you remove the absolute-value bars, well, remember that the absolute valute of a quantity is its distance from zero on the number line. There are always two answers to this, the one to the left of the zero and the one to the right of zero.
Take, for example the absolute of negative five, written as: |-5|.
You know the answer is 5, that is, the absolute value of -5, |-5| is a distance of 5 from zero on the number line. But there are two integers that fit this description, namely 5 and -5.
To check the solutions, try values for r in the appropriate range for each inequality.
Try r > 5, or r = 6
|2(6)+9|>19
|12+9|>19
|21|>19
Try r < -14 or r = -15
|2(-15) + 9| > 19
|-30 + 9| > 19
|-21| > 19
|
|
|