SOLUTION: I am having real trouble grasping the concepts. Topic: Solving Trigonometric Equations Q: Find all solutions of {{{ sin( 2x ) = -sqrt( 3 )/2 }}} in the interval [0,2pi) Answe

Algebra ->  Trigonometry-basics -> SOLUTION: I am having real trouble grasping the concepts. Topic: Solving Trigonometric Equations Q: Find all solutions of {{{ sin( 2x ) = -sqrt( 3 )/2 }}} in the interval [0,2pi) Answe      Log On


   

Question 768031: I am having real trouble grasping the concepts.
Topic: Solving Trigonometric Equations
Q:
Find all solutions of +sin%28+2x+%29+=+-sqrt%28+3+%29%2F2+ in the interval [0,2pi)
Answer Choices:
1. None of these
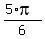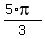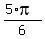2. +x+=+pi%2F3+ , +%284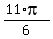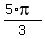%2Api%29%2F3+ , +%285%2Api%29%2F6+ , +%287%2Api%29%2F6+
3. +x+=+%282%2Api%29%2F3+ , +%285%2Api%29%2F3+ , +%285%2Api%29%2F6+ , +%2811%2Api%29%2F6+
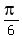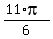
4. +x+=+pi%2F3+ , +%285%2Api%29%2F3+ , +pi%2F6+ , +%2811%2Api%29%2F6+
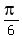5. +x+=+%282pi%29%2F3+ , +%284%2Api%29%2F3+ , +pi%2F6+ , +%287%2Api%29%2F6+
Please note: I am only showing ans choices as a frame of reference; I'm more interested in a detailed review of how to work the problem. Also, do I need to draw a unit circle?
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Find the two points on the unit circle illustrated where the -coordinate is equal to .



Now, has to be in the interval [), but that means is in the interval [). Hence the two points you found on the circle are actually 4 possibilities for the value of , namely . Divide each possibility for by 2, and you will have 4 numbers that match one of your answer choices.

John

Egw to Beta kai to Sigma
My calculator said it, I believe it, that settles it
The Out Campaign: Scarlet Letter of Atheism