In order to factor 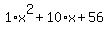 , first we need to ask ourselves: What two numbers multiply to 56 and add to 10? Lets find out by listing all of the possible factors of 56 , first we need to ask ourselves: What two numbers multiply to 56 and add to 10? Lets find out by listing all of the possible factors of 56
Factors:
1,2,4,7,8,14,28,56,
-1,-2,-4,-7,-8,-14,-28,-56,List the negative factors as well. This will allow us to find all possible combinations
These factors pair up to multiply to 56.
1*56=56
2*28=56
4*14=56
7*8=56
(-1)*(-56)=56
(-2)*(-28)=56
(-4)*(-14)=56
(-7)*(-8)=56
note: remember two negative numbers multiplied together make a positive number
Now which of these pairs add to 10? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 10
| First Number | | | Second Number | | | Sum | | 1 | | | 56 | || | 1+56=57 | | 2 | | | 28 | || | 2+28=30 | | 4 | | | 14 | || | 4+14=18 | | 7 | | | 8 | || | 7+8=15 | | -1 | | | -56 | || | -1+(-56)=-57 | | -2 | | | -28 | || | -2+(-28)=-30 | | -4 | | | -14 | || | -4+(-14)=-18 | | -7 | | | -8 | || | -7+(-8)=-15 | substitute a=3 and b=7
So the equation becomes:
(x+3)(x+7)
Notice that if we foil (x+3)(x+7) we get the quadratic 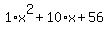 again
None of these factors add to 10. So this quadratic cannot be factored. In order to solve for x, we need to use the quadratic formula. again
None of these factors add to 10. So this quadratic cannot be factored. In order to solve for x, we need to use the quadratic formula.
So the quadratic 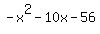 cannot be factored cannot be factored
|
|