SOLUTION: show that x^2+(3k-2)x+k(k-1)=0 has real roots for all value of k

Algebra ->  Systems-of-equations -> SOLUTION: show that x^2+(3k-2)x+k(k-1)=0 has real roots for all value of k      Log On


   

Question 766741: show that x^2+(3k-2)x+k(k-1)=0 has real roots for all value of k
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
A quadratic equation is ax%5E2+%2B+bx+%2B+c. Remember that a quadratic equation has real roots if the discriminant is greater than or equal to 0. The discriminant is b%5E2+-+4ac.


For the given equation b = 3k - 2 and b%5E2+=+9k%5E2+-+12k+%2B4


a = 1 and c = k(k-1) = 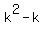k%5E2+-+k


The discriminant is therefore (((9k^2 - 12k +4 - 4k^2 +4k = 5k^2 -8k +4}}}


That is a quadratic equation with a=5, b = -8 and c =4. It has to be greater than or equal to 0 in order for the original equation to have real roots for all values of k.


The discriminant of this equation is 64-80 = -16. That means this equation has no real roots. In other words, it's a parabola that never crosses the x-axis (it has no real zeroes.) Since a is positive, we know the parabola opens up. Since it opens up, and it never crosses the x-axis, its values are all positive.


Since the discriminant of the original equation is itself a parabola with only positive values, the original equation has a positive discriminant, and thus only real roots.