|
Question 76661: Ed and Dave are going to divide a case prize of $14,000 in a ratio of 2 to 5. How much will Dave receive?
I came up with 8,000. I am not sure this is correct. Could you verify this for me? Thanks.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, let's see.
.
The total prize is $14,000. Let's call Dave's share D and Ed's share E. The sum of the two
shares has to total the entire prize. So we can write the equation:
.
D + E = 14,000
.
And by subtracting D from both sides of this equation we can see that Ed's share is:
.
E = 14,000 - D
.
So we can set up the ratio of Ed's share (14,000 - D) to Dave's share (D) and get:
.

.
but the problem also tells us that this ratio is 
.
So we can set up the equation:
.

.
When you have two ratios equal to each other, a method of solving them is to find the
cross products and set them equal. The cross products come from multiplying the numerator of
one ratio times the denominator of the other ratio. Then multiply the denominator of
the first ratio times the numerator of the second ratio.
.
In this problem the first cross product is
.
 <--- numerator of first ratio times denominator of second <--- numerator of first ratio times denominator of second
.
and this multiplication results in 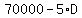 . .
.
and the second cross product is the denominator of the first ratio (D) times the numerator of
the second ratio (2) to get 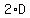 . .
.
[You may be able to see why they are often referred to as cross products. You are multiplying
along diagonals drawn through the equal sign between the two ratios.]
.
Anyhow, set the two cross products equal and you get:
.

.
Solve by adding 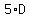 to both sides to eliminate the to both sides to eliminate the 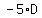 on the left side. This on the left side. This
results in:
.

.
Solve for Dave's share by dividing both sides by 7 to get:
.

.
So Dave gets $10,000 which means that Ed gets the remaining $4,000 of the prize.
.
Now check to see that the ratio is correct. Ask yourself, is $4,000 divided by $10,000
the same as  ? If you divide both the numerator and the denominator by 2,000 you ? If you divide both the numerator and the denominator by 2,000 you
find that 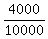 does, in fact, reduce to does, in fact, reduce to  . Therefore, our answer is . Therefore, our answer is
correct.
.
If you do the same verification with your answer in which Dave got $8000 and Ed got the
remaining $6000 your ratio is 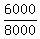 which is which is  and that reduces to and that reduces to
 not not  as required by the problem. as required by the problem.
.
Hope this helps you to see your way through the problem and perhaps introduces you to
using cross products to solve proportions (two ratios set equal).
|
|
|
| |