SOLUTION: A regular pentagon has sides of 20 cm. an inner pentagon with sides of 10 cm is inside and concentric to the larger pentagon. What is the area inside the larger pentagon and outsid

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: A regular pentagon has sides of 20 cm. an inner pentagon with sides of 10 cm is inside and concentric to the larger pentagon. What is the area inside the larger pentagon and outsid      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 766552: A regular pentagon has sides of 20 cm. an inner pentagon with sides of 10 cm is inside and concentric to the larger pentagon. What is the area inside the larger pentagon and outside the smaller pentagon?
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
A regular pentagon has sides of 20 cm. an inner pentagon with sides of 10 cm is inside and concentric to the larger pentagon. What is the area inside the larger pentagon and outside the smaller pentagon?
---------
For a regular polygon with n sides of length s:
Area+=+ns%5E2%2Acot%28180%2Fn%29%2F4
For s = 20:
Area+=+5%2A400%2Acot%2836%29%2F4+=+500%2Acot%2836%29
The area of the 10 cm = 1/4 of the 20 = 125%2Acot%2836%29
Area between = 375*cot(36)
=~ 516.143 sq cm

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Here is a different approach.  It's longer but it doesn't
use the formula for the area of a regular polygon,
which is not usually studied in a geometry or trig class.
The following way only uses the interior angle formula,
the tangent equation, and the area of a trapezoid (or 
trapezium) formula.
 
Each interior angle of an n-sided regular polygon is

%28%28n-2%29%2A%22180%B0%22%29%2Fn = %28%285-2%29%2A%22180%B0%22%29%2F5 = 108° 



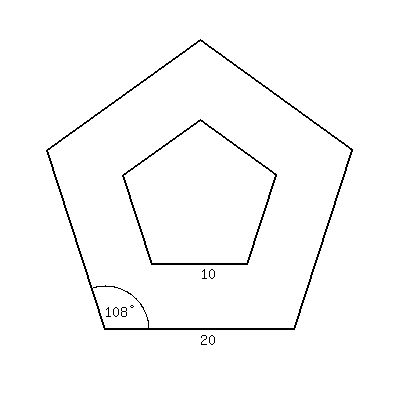
Then we draw in two vertical lines in red, which divide
the 20cm side into 5cm, 10cm, and 5cm lengths:


In the right triangle, we find h from

tan(54°) = 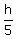h%2F5

h = 5·tan(54°)

Area of trapezoid = 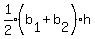expr%281%2F2%29%28b%5B1%5D%2Bb%5B2%5D%29%2Ah = expr%281%2F2%29%2810%2B20%29%2A5%2Atan%28%2254%B0%22%29

Area of all 5 trapezoids = 5%2Aexpr%281%2F2%29%2810%2B20%29%2A5%2Atan%28%2254%B0%22%29 = 516.1432202 cm²

Edwin