|
Question 76649: I need to solve for x. I believe the answer if 4 but I have no idea how to start.
(2x-3/x-1)-(x-1/x+2)=(2x-5/x+2)+(2-x/1-x)
Found 2 solutions by psbhowmick, bucky:
Answer by psbhowmick(878)   (Show Source): (Show Source):
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sort of a long problem. Given:
.

.
Notice that the denominators are (x - 1), (x + 2), and (1 - x). Sure would be nice if
that denominator (1 - x) was (x - 1) so it was like the other one. So let's apply a little
math trick to the last term on the right side. Let's multiply the numerator and the denominator
inside the parentheses by 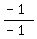 . Since the numerator and the denominator of that multiplier . Since the numerator and the denominator of that multiplier
are equal, it is the same as multiplying the fraction inside the parentheses by 1, so it does
not change anything ... except it reverses the signs of the terms in the parentheses.
When you do that manipulation, the last term on the right side becomes:
.
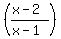
.
and the equation becomes:
.

.
Now we're ready to rumble! Let's multiply every term on both sides by the product of
the common terms in the denominator. In other words, let's multiply everything by the
product (x-1)*(x+2). When we do, the problem becomes:
.

.
Now we can cancel any terms in the denominator that have the same term in the numerator as
shown:
.

.
And the problem is reduced to:
.

.
This is now just an "ordinary" algebraic equation. Let's multiply out the all the terms to
get:
.

.
Remove the parentheses. If they are preceded by a + sign, just erase them. If they are
preceded by a minus sign, when you remove them, change the sign of all the terms inside. When
you remove the parentheses you get:
.

.
Grouping like terms on the left and right side results in:
.

.
Combining like terms gives you:
.

.
Since this is going to be a quadratic equation, let's get it into standard form by moving
everything to the left side and just have a zero on the right side. Do this by subtracting
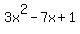 from both sides. After grouping like terms on the left side, this from both sides. After grouping like terms on the left side, this
subtraction results in:
.

.
Combine like terms to get:
.

.
Simplify by dividing both sides by -2:
.

.
This quadratic factors to:
.

.
and this equation will be true if either factor on the left side is zero. So one at a
time set the factors equal to zero and solve for x.
.
 Solve by adding 4 to both sides to get Solve by adding 4 to both sides to get 
.
Next:
.
 Solve by adding 1 to both sides to get Solve by adding 1 to both sides to get 
.
But this last solution has to be ignored. Why??? Go way back to the original problem and
note what happens if x = 1. If it does = 1 then a couple of the denominators become
zero, and division by zero is not allowed. Therefore, x = 1 is not a valid answer. The
only acceptable answer is x = 4.
.
You can check that by returning to the original problem and substituting 4 for x to see if
the left side of the equation still equals the right side. You should find that it does.
.
Hope this helps you to see your way through the problem.
|
|
|
| |