Question 766398: Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.
f(x) = x2 + 2x - 9
A) minimum;
B) maximum;
C) maximum;
D) minimum;
2. Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.
f(x) = -x2 - 2x - 6
A) minimum;
B) minimum;
C) maximum;
D) maximum;
3. Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.
f(x) = -3x2 + 6x
A) maximum;
B) minimum;
C) minimum;
D) maximum;
4. Find the degree of the polynomial function.
f(x) = -2x + 7x2
A) 2
B) 7
C) -2
D) 1
5. Find the degree of the polynomial function.
f(x) =
A) 3
B) 0
C) -
D) 4
6. Find the degree of the polynomial function.
f(x) = πx5 - 6x4 - 9
A) 1
B) 5
C) π
D) 4
7. Find the degree of the polynomial function.
f(x) = 5x - x6 +
A) 5
B) 6
C) 1
D) -1
8. Find the degree of the polynomial function.
g(x) = -7x3 + 9
A) 0
B) -7
C) 3
D) 4
9. Find the degree of the polynomial function.
h(x) = -19x + 4
A) 1
B) 0
C) -19
D) 2
10. Find the degree of the polynomial function.
17x3 + 3x2 - 2x - 2y4 - 1
A) 17
B) 10
C) 3
D) 4
11. Find the degree of the polynomial function.
f(x) = -14x3 + 9x2 - 2
A) 6
B) 9
C) 3
D) -14
12. Find the zeros of the polynomial function.
f(x) = x3 + x2 - 42x
A) x = - 7, x = 6
B) x = 0, x = 5, x = 6
C) x = 5, x = 6
D) x = 0, x = - 7, x = 6
13. Find the zeros of the polynomial function.
f(x) = x3 + 3x2 - x - 3
A) x = - 3, x = 3
B) x = -1, x = 1, x = - 3
C) x = 9
D) x = 1, x = - 3, x = 3
14. Find the zeros of the polynomial function.
f(x) = x3 - 6x2 + 9x
A) x = 0, x = 3
B) x = 0, x = -3, x = 3
C) x = 1, x = 3
D) x = 0, x = -3
15. Find the zeros of the polynomial function.
f(x) = x3 + 4x2 - 9x - 36
A) x = -3, x = 3
B) x = 4, x = -3, x = 3
C) x = -4, x = 9
D) x = -4, x = -3, x = 3
16. Find the zeros of the polynomial function.
f(x) = 2(x + 2)(x - 4)4
A) x = 2, x = -4, x = 4
B) x = 2, x = 4
C) x = -2, x = 4
17. Find the vertical asymptotes, if any, of the graph of the rational function.
g(x) =
A) x = 0 and x = -3
B) x = 1 and x = -3
C) x = -3
D) no vertical asymptote
18. Find the vertical asymptotes, if any, of the graph of the rational function.
f(x) =
A) x = 0 and x = 1
B) x = 0 and x = -1
C) x = 1
D) no vertical asymptote
19. Find the vertical asymptotes, if any, of the graph of the rational function.
f(x) =
A) x = 4
B) x = -4
C) x = -4, x = 4
D) no vertical asymptote
20. Find the vertical asymptotes, if any, of the graph of the rational function.
g(x) =
A) x = 4, x = -4
B) x = 4
C) x = 4, x = -4, x = 0
D) no vertical asymptote
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question 730086
1.
Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.

Coefficient of the x^2 term is +, --> a minimum
The vertex is on the LOS, Line of Symmetry, which is



plug it in  and find and find 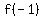



Vertex is at ( , , ) )
=====================
A) minimum; (-10,-1)
B) maximum; (-1,-10)
C) maximum; (-10,-1)
D) 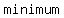 ; (-1,-10) ; (-1,-10)
2.
Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.





plug it in  and find and find 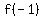



Vertex is at ( , , ) and it is a maximum ) and it is a maximum
A) minimum; (-5,-1)
B) minimum; (-1,-5)
C) 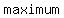 ; (-1,-5) ; (-1,-5)
D) maximum; (-5,-1)
3.
Determine whether the given quadratic function has a minimum value or maximum value. Then find the coordinates of the minimum or maximum point.





plug it in  and find and find 



Vertex is at ( , , ) and it is a maximum ) and it is a maximum
A) maximum; (-1,-3)
B) minimum; (1,3)
C) minimum; (-1,-3)
D) 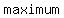 ; (1,3) ; (1,3)
2 & 3 same as #1
=================
4.
Find the degree of the polynomial function.

A) 2
B) 7
C) -2
D) 1
5.
answer: A) 
______
A) 3
B) 0
C) -
D) 4
answer: D) 
A) 1
B) 5
C) π
D) 4
answer: B) 
7.
Find the degree of the polynomial function.

A) 5
B) 6
C) 1
D) -1
answer: B) 
8.
Find the degree of the polynomial function.

A) 0
B) -7
C) 3
D) 4
answer: C) 
9.
Find the degree of the polynomial function.

A) 1
B) 0
C) -19
D) 2
answer: A) 
10.
Find the degree of the polynomial function.
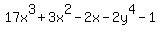
A) 17
B) 10
C) 3
D) 4
answer: D) 
11.
Find the degree of the polynomial function.

A) 6
B) 9
C) 3
D) -14
===============
Degree is the highest exponent of the variable.
answer: C) 
|
|
|