|
Question 76625: The diameter of the Milky Way disc is approximately 9 x 10^20 meters. How long does it take light, traveling at 10^16 m/year to travel across the diameter of the Milky Way?
900,000 years
90,000 years
9,000 years
900 years
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can use the standard equation for distance (D) when a rate (or speed) R is involved and
so is the time (T) that the rate will be in effect. The equation is:
.

.
In this problem, the distance (D) and the rate (R) of travel are given, and you are asked
to solve for the time involved.
.
To solve for T, divide both sides of the equation by R and the equation becomes:
.

.
You are given that D, the distance, is 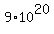 and the rate of light is and the rate of light is  . .
Note that I added the multiplier 1 to the exponential value of 10 for the rate that light
is traveling. And always be sure to check that the units involved are compatible.
In this case the distance is in meters, the rate is in meters per year, and the answer is to
be in years. We have no inconsistencies in units so we don't have to do any conversions.
All distances are in meters and all times are in years.
.
Take the equation for time and substitute the values of D and R and you get:
.

.
We sort of split this into two problems .... divide the 9 by the 1 and also divide the
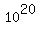 by the by the  . Recall that when you divide a base with an exponent by . Recall that when you divide a base with an exponent by
the same base with an exponent, the answer is the same base with the difference between
the exponents. Maybe the work will give you the idea:
.

.
The 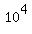 part of the answer tells you that it is 10,000. part of the answer tells you that it is 10,000.  , ,  , ,
 , and , and  . So we can say that the answer is 9 times 10,000 . So we can say that the answer is 9 times 10,000
which is 90,000 and the units is years. So the correct answer is the second one down in
your list of answers ... 90,000 years.
.
Hope the problem has taught you a couple of things ... first the equation for distance when
rate and time are involved. And second, how to divide numbers that are in the form of
scientific notation ... an integer times ten raised to a power divided by an integer times
ten raised to a power ... divide the integers and raise ten to the difference of the two
exponents ... and the difference is found by subtracting the exponent in the denominator from
the exponent in the numerator.
|
|
|
| |