SOLUTION: Give all solutions of each nonlinear system of equations: x^2+y^2=9, |x|=|y|

 x²+y² = 9, 
   |x| = |y|

Square both sides of the second equation

    x² = y²

Substitute y² for x² in the first equation:

 y² + y² = 9
     2y² = 9
      y² = 
       y =  =  =  =  = 

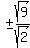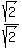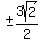And since x² = y², x also =  

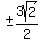So the four possible solutions are:

(,), (,), (,), (,)

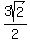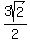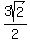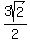All four check, so all four are solutions.

The graph of x²+y²=9 is this circle


and the graph of |y|=|x| is the pair of graphs y = |x| and y = -|x|

 and

which together are



Put them together on the same graph and you get:



The four points of intersection are 

(,), (,), (,), (,)

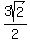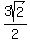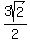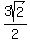Edwin