SOLUTION: Please help me determine a formula for the nth term of a geometric sequence where term 1 = 4 and term 13 = 16 384

Algebra ->  Sequences-and-series -> SOLUTION: Please help me determine a formula for the nth term of a geometric sequence where term 1 = 4 and term 13 = 16 384      Log On


   

Question 765510: Please help me determine a formula for the nth term of a geometric sequence where term 1 = 4 and term 13 = 16 384
Answer by ramkikk66(644) About Me  (Show Source):
You can put this solution on YOUR website!

1st term = 4, 13th term = 16384

In a geometric progression (GP), every term is got by multiplying the previous
term by a common ratio (r).

So if a is the 1st term, r is the common ratio
1st term = a
2nd term = a*r
3rd term = a*r*r = a*r^2
In general, nth term will be 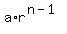a%2Ar%5E%28n-1%29

Here we need to find what is the common ratio.

a = 4, 13th term = 4%2A%28r%29%5E%2812%29+=+16384


r%5E12+=+16384%2F4+=+4096

r+=+4096%5E%281%2F12%29+=+2 (you can find it using a calculator, or by factorizing 4096)

So, a = 4 and r = 2 in this series.

Formula for nth term = 4%2A2%5E%28n-1%29+=+2%5E2%2A2%5E%28n-1%29+=+2%5E%28n%2B1%29

Hope you got it :)