Question 765330: Help me solving a linear programs?
A tailor sews 2 kinds of shirt to be sold, the first kind needs 2 m of cotton and 4 m of silk, and the second kind needs 5 m of cotton and 3 m of silk. There are 70 m of cotton and 84 m of silk available. The first kind of shirt is sold at IDR 25,000.00 profit and the second shirt is sold at IDR 50,000.00 profit. To maximize his profit, he must sell?
Correct me if I'm wrong, the equations are;
For shirt A : 2x + 4y = 25000
For shirt B : 5x + 3y = 50000
And maximum profit function / f(x, y) is;
x + y ≤ 154
If it is so, after eliminating both equation I don't get square number, I got comas/decimal. Thus when I substitute to f(x,y) I don't get the answer.
Please advise me how to solve this. Sorry if I put this on wrong category.
Thanks :)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your objective function is:
25,000 * x + 50,000 * y
x is the number of shirts of type 1.
y is the number of shirts of type 2.
25,000 is the profit per shirt of type 1.
20,000 is the profit per shirt of type 2.
your constraint functions are:
2x + 5y <= 70
4x + 3y <= 84
there are 2 meters of cotton per shirt of type 1 and 5 meters of cotton per shirt of type 2.
there are 4 meters of silk per shirt of type 1 and 3 meters of silk per shirt of type 2.
x and y both have to be greater than or equal to 0.
you graph the constraint equation to get the following graph:
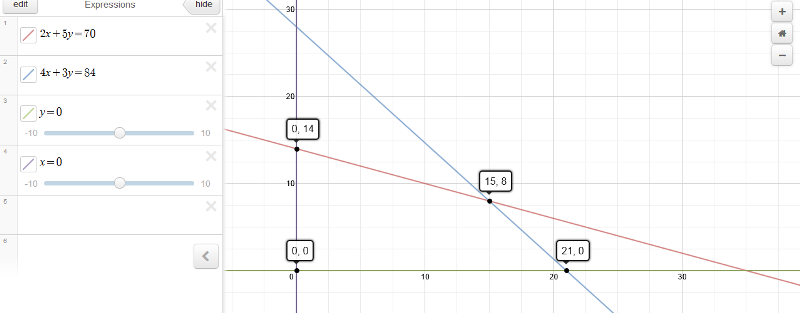
your feasible region is above the line x = 0 and to the right of the line y = 0 and below the lines of 2x + 5y <= 70 and 4x + 3y = 84.
this feasible region is bounded by the lines between the following points:
(0,14)
(15,8)
(21,0)
(0,0)
the objective function will be maximum at one of these points.
calclate the objective function at each of these points and you will get:
(0,14) = 280,000
(15,8) = 535,000
(21,0) = 525,000
(0,0) = 0
you have maximum profit at the point (15,8).
at this point, the value of x is equal to 15 and the value of y is equal to 8
25,000 * 15 + 20,000 * 20,000 = $535,000.
at the intersection point of (15,8), the constraints on cotton are:
2x + 5y <= 70
2x + 5y becomes 2(15) + 5(8) = 70
the constraints on cotton are satisfied.
at the intersection point of (15,8), the constraints on silk are:
4x + 3y <= 84
4x + 3y becomes 4(15) + 3(8) = 84
the constraints on silk are satisfied.
you mixed up your constraints with your objective function.
the objection function was to maximize profit.
profit = 25,000 * x + 20,000 * y
constraints are separate equations.
you graph the constraints.
you find the intersection points of the feasible region.
you analyze the objective function at the intersection points of the feasible region.
the intersection point with the maximum value evaluated from the profit equation is the solution you are looking for.
|
|
|