Question 765278: i need help finding the center, vertices, and foci of this equation 9x^2+36(y-2)^2-324=0
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 



 or or

this is an ellipse with  and and  ; so, the center is at ; so, the center is at
( , , ) )
we also know that semi-major axis  and semi-minor axis and semi-minor axis  ; so, we have an ellipse with horizontal major axis ; so, we have an ellipse with horizontal major axis
vertices:
(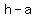 , , ) =>( ) =>( , , )=>( )=>( , , ) )
(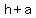 , , )=>( )=>(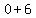 , , )=>( )=>( , , ) )
c0-vertices:
( , ,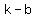 ) =>( ) =>( , , )=>( )=>( , , ) )
( , ,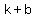 )=>( )=>( , ,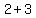 )=>( )=>( , , ) )
foci:
The formula generally associated with the focus of an ellipse is

so,  and and 




 and and 
so, foci is at (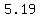 , , ) and ( ) and (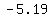 , , ) )

|
|
|