SOLUTION: The coordinates of {{{A}}} and {{{B}}} are (2,-4) and (0,3) respectively. {{{C}}} is a point on the line {{{L}}} such that the area of the triangle {{{ABC}}} is {{{8 unit^2}}}. Fin

Algebra ->  Triangles -> SOLUTION: The coordinates of {{{A}}} and {{{B}}} are (2,-4) and (0,3) respectively. {{{C}}} is a point on the line {{{L}}} such that the area of the triangle {{{ABC}}} is {{{8 unit^2}}}. Fin      Log On


   

Question 764907: The coordinates of A and B are (2,-4) and (0,3) respectively. C is a point on the line L such that the area of the triangle ABC is 8+unit%5E2. Find the two possible equation of L.
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Line AB is y=-(7/2)x+3, and the line perpendicular to it at point (0,3) is y=(2/7)x+3. The point (0,3) here was picked arbitrarily for convenience.

Using segment AB as a base of the triangle, distance formula, steps here omitted,... the base AB is 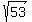sqrt%2853%29.
Triangle with 8 unit^2 will have an altitude value h, so that:
%281%2F2%29%28sqrt%2853%29%29%2Ah=8
highlight%28h=16%2Fsqrt%2853%29%29

What point is h units away from (0,3) and is on line y=(2/7)x+3?
That refers to another distance and the use of distance formula again.
We want those two, variable points of (x, (2/7)x+3).
Applying distance formula,
h=16%2Fsqrt%2853%29=sqrt%28%28x-0%29%5E2%2B%28%282%2F7%29x%2B3-3%29%5E2%29
which will simplify to:
.
.
highlight%28x=-112%2F53%29 or highlight%28x=112%2F53%29
From those two values, you can use y=%282%2F7%29x%2B3 to determine the corresponding values for y.

Can you finish the rest of the way to the needed line y=-%287%2F2%29x%2Bg for some y-intercept g ?


------------------------------------------
Just to show final answer without the remaining steps,
lines wanted are:
highlight%28y=-%287%2F2%29x%2B519%2F53%29 and highlight%28y=-%287%2F2%29x%2B11%29
and know that point C is really still a variable point.