Question 764740: Suppose that the equation p(x) = -4x2 + 400x - 1000, where x represents the number of items sold, describes the profit function for a certain business. How many items should be sold to maximize the profit?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITHOUT MEMORIZED FORMULAS OR NAMES:
The function  can be re-written in a form that gives you a better understanding (and the answer to the problem. can be re-written in a form that gives you a better understanding (and the answer to the problem.
 --> -->  --> -->  --> --> 
When  the firt term is zero the firt term is zero 
and  . .
For any other value of  , , 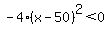 and and 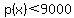 , ,
so  is the number of items sold that maximizes the profit, is the number of items sold that maximizes the profit,
and  is the maximum profit possible. is the maximum profit possible.
WITH WORDS AND FORMULAS TO MEMORIZE:
 is a is a  function (meaning a polynomial of degree 2). function (meaning a polynomial of degree 2).
A quadratic function, like  
graphs as a  and has a maximum or a minimum (the and has a maximum or a minimum (the  of the parabola). of the parabola).
If the leading coefficient is negative, the function has a maximum. Otherwise, it's a minimum.
Quadratic functions are of the form 
(or  when in vertex form). when in vertex form).
The number you want to find is  , the x-coordinate of the vertex of the parabola, which is part of , the x-coordinate of the vertex of the parabola, which is part of
 , the equation of the axis of symmetry of the parabola. , the equation of the axis of symmetry of the parabola.
If your teacher insist on memorization of formulas, you may have to memorize  , and for your problem you would write , and for your problem you would write
 , ,  --> -->  --> --> 
|
|
|