|
Question 764150: Please help me! I have struggled with this problem for days and have not gotten anywhere with it.
A manufacturing company produces four different models of integrated circuits. Each type of circuit requires material, labor, and machine time. The optimal combination of the four types of circuits is limited by the constraints of availability for these three resources. The formulation of the linear programming production problem is:
Maximize Z = 12x1 + 10x2 + 15x3 + 11x4 (objective function for profit)
Subject to the following constraints:
Material: 5x1 + 3x2 + 4x3 + 2x4 = 240 pounds
Machine time: 6x1 + 8x2 + 2x3 + 3x4 = 240 hours
Labor: 2x1 + 3x2 + 3x3 + 2x4 = 180 hours
Nonnegativity: x1, x2, x3, x4 = 0
Where: x1 = quantity of Product 1 produced
x2 = quantity of Product 2 produced
x3 = quantity of Product 3 produced
x4 = quantity of Product 4 produced
Use Microsoft Excel and Solver to find the optimal solution for the production problem. Be sure that values selected by the computer are integers (as it doesn't make any sense to discuss producing part of a unit of a product).
Include your interpretation of the results by stating:
• How many of each product will be produced?
• What is the profit for the optimal solution?
• What resource(s) is limiting the production?
I really don't know how to set this problem up to use Excel solver. If someone could point me in the right directions would be a big help.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! excel solver was used to find your result.
maximum profit is achieved when you produce 12 type x3 and 72 type x4.
maximum profit is 972.
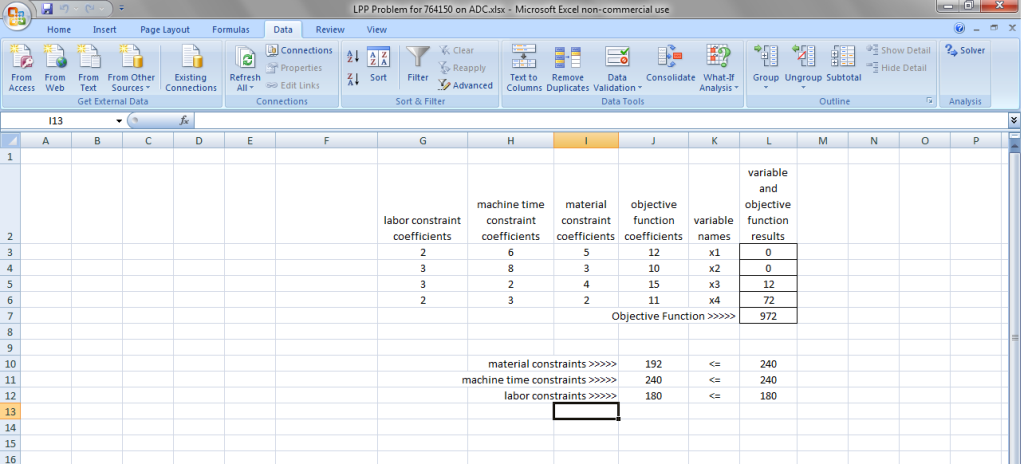
excel results are shown in the attached picture of the excel file.
the solver setup is shown in the attached picture.

the solver setup options are shown in the attached picture.

there are several websites that can help you learn how to use excel.
one such website is at:
http://cs.stfx.ca/~ltyang/csci-235/labs/Linear_Programming_Using_Excel.pdf
a very brief tutorial follows;
the objective function is in cell L8
the formula in cell L8 is: =SUMPRODUCT(J3:J6,L3:L6)
this function takes the cell j3 and multiplies by l3, j4 and multiplies by l4, j5 and multiplies it by l5, j6 and multiplies it by l6 and then adds them all up.
the cells j3 to j6 contain the coefficdients used to find the profit.
the cells l3 to l6 contain the values for the variables that the excel solver is calculating.
the constraints are in cells l10 to l12.
the values that the excel solver calculates are in cells j10 to j12.
the formulas in cells j10 to j12 are used to determine the values for the individual constraints.
for example, the formula in cell j10 is: =SUMPRODUCT(I3:I6,L3:L6)
this formula is multiplying the values in cell i3 * the values in cell l3, then cell i4 * cell l4, then cell i5 * cell l5, then cell i6 * cell l6, and then adding them up. these are the constraints for material.
while the cells are being shown compared on the spreadsheet, the actual constraints that are used by the excel solver are in the solver set up page.
there are additional constaints in the solver setup page, like forcing the values of the variables that can be adjusted by the excel solver to be integer and also making an assumption that all values not explicitly shown to be greater than or equal to 0 are 0 (this in the excel setup options page.
anyway, take a look.
between what is here and what you can find on the web, you should be able to figure it out
just do a search on (excel 2007 solver tutorials) or (how to use excel solver) and you should be lots of websites, some of which are actually useful.
i think if you go to help in excel and put in solver, you'll also get some additional help topics to assist you.
if you want the excel file, let me know and i'll email it to you.
theoptsadc@yahoo.com
how many of each product is produced is shown by excel (cells L3 to L6).
objective function is in cell L8.
resources limiting production appear to be machine time constraints and labor constraints.
if you increase the amount of hours available to each, your profit goes up and your material constraints can be maximally utilized.
figuring that out is tricky, though, because the objective function changes when you change the constraints so you don't have the same results anymore.
|
|
|
| |