We want the shorter diagonal BD,
but first we must calculate the longer diagonal,
the green line AC below:
 We use the law of cosines on ΔABC since this is the SAS case:
AC² = AB² + BC² - 2·AC·BC·cos(∠ABC)
AC² = 1.2² + 1.6² - 2(1.2)(1.6)cos(140°)
AC = 2.634693656 m
We use the law of sines to find ∠BAC
We use the law of cosines on ΔABC since this is the SAS case:
AC² = AB² + BC² - 2·AC·BC·cos(∠ABC)
AC² = 1.2² + 1.6² - 2(1.2)(1.6)cos(140°)
AC = 2.634693656 m
We use the law of sines to find ∠BAC
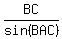


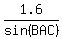

 Cross multiply:
(2.634693656)sin(∠BAC) = (1.6)sin(140°)
sin(∠BAC) =
Cross multiply:
(2.634693656)sin(∠BAC) = (1.6)sin(140°)
sin(∠BAC) =  ∠BAC = 22.97645649°
Now that we have ∠BAC we draw half the shorter diagonal BE,
which is perpendicular to the longer diagonal AC, in red:
∠BAC = 22.97645649°
Now that we have ∠BAC we draw half the shorter diagonal BE,
which is perpendicular to the longer diagonal AC, in red:
 Since ΔABE is a right triangle:
Since ΔABE is a right triangle:
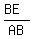 =
=  = sin(BAC)
BE = AB·sin(BAC)
BE = 1.2·sin(22.97645649°)
BE = 0.4684234191 m
So the entire shorter diagonal, BD,
= sin(BAC)
BE = AB·sin(BAC)
BE = 1.2·sin(22.97645649°)
BE = 0.4684234191 m
So the entire shorter diagonal, BD,
 is twice the length of BE, so
BD = 2·BE = 2(0.4684234191) = 0.9368468381 m
Rounded to tenths: 0.9 m
Edwin
is twice the length of BE, so
BD = 2·BE = 2(0.4684234191) = 0.9368468381 m
Rounded to tenths: 0.9 m
Edwin